ОБРА́ТНАЯ СВЯЗЬ

Рис. 1. Блок-схема системы с обратной связью; Uвх и Uвых – сигналы на входе и выходе системы.

ОБРА́ТНАЯ СВЯЗЬ, об­рат­ное воз­дей­ст­вие ре­зуль­та­тов к.-л. про­цес­са на его про­те­ка­ние в сис­те­мах разл. при­ро­ды или воз­дей­ст­вие уп­рав­ляе­мо­го про­цес­са на уп­рав­ляю­щий ор­ган. О. с. осу­ще­ст­в­ля­ет­ся ли­бо с по­мо­щью внеш­ней це­пи, ли­бо за счёт внутр. уст­рой­ст­ва сис­те­мы. Сис­те­мы с О. с. час­то пред­став­ля­ют в ви­де схе­мы, на ко­то­рой сиг­нал с вы­хо­да лю­бо­го уст­рой­ст­ва по­сту­па­ет на его вход (рис. 1).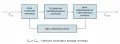 Ес­ли на­чаль­ное от­кло­не­ние к.-л. ха­рак­те­ри­сти­ки про­цес­са от её ис­ход­но­го зна­че­ния при­во­дит к даль­ней­ше­му рос­ту это­го от­кло­не­ния, то О. с. на­зы­ва­ет­ся по­ло­жи­тель­ной, в про­ти­во­по­лож­ном слу­чае – от­ри­ца­тель­ной. По­ло­жи­тель­ная О. с. при­во­дит к то­му, что воз­ник­шее от­кло­не­ние со­стоя­ния сис­те­мы всё бо­лее уве­ли­чи­ва­ет­ся и сис­те­ма мо­жет стать не­ус­той­чи­вой. Тер­мин «О. с.» ши­ро­ко ис­поль­зу­ет­ся для опи­са­ния эф­фек­тов в фи­зич., хи­мич., био­ло­гич., ин­фор­мац., эко­но­мич., со­цио­ло­гич. и др. сис­те­мах. О. с. иг­ра­ет клю­че­вую роль в ки­бер­не­ти­ке, осо­бен­но в тео­рии ав­то­ма­тич. управ­ле­ния.

Тер­мин «О. с.» пер­во­на­чаль­но поя­вил­ся в ра­дио­тех­ни­ке, где им обо­зна­ча­лось элек­трич. воз­дей­ст­вие анод­ной це­пи лам­по­во­го уси­ли­те­ля элек­трич. ко­ле­ба­ний на цепь сет­ки уси­ли­ваю­щей лам­пы. Ес­ли из­ме­не­ния то­ка в анод­ной це­пи пе­ре­да­ют­ся на се­точ­ную цепь в фа­зе с из­ме­не­ния­ми то­ка в этой це­пи, то уси­ле­ние воз­рас­та­ет (по­ло­жи­тель­ная О. с.). В слу­чае дос­та­точ­но боль­шой по­ло­жи­тель­ной О. с. ра­нее ус­той­чи­вые ха­рак­те­ри­сти­ки сис­те­мы мо­гут при­нять ха­рак­тер ко­леб­лю­щих­ся ве­ли­чин – воз­ни­ка­ют ав­то­ко­ле­ба­ния. Ес­ли из­ме­не­ния то­ка в анод­ной це­пи пе­ре­да­ют­ся в се­точ­ную цепь в про­ти­во­фа­зе с из­ме­не­ния­ми то­ка в этой це­пи, то уси­ле­ние умень­ша­ет­ся (от­ри­ца­тель­ная О. с.), но по­вы­ша­ет­ся ус­той­чи­вость уси­ли­те­ля к внеш­ним воз­дей­ст­ви­ям.

Рис. 2. Контур управления, реализующий отрицательную обратную связь.

Про­стей­шим при­ме­ром сис­те­мы с по­ло­жи­тель­ной О. с. яв­ля­ет­ся уси­ли­тель с гром­ко­го­во­ри­те­лем, зву­ко­вой сиг­нал ко­то­ро­го воз­дей­ст­ву­ет на мик­ро­фон, под­клю­чён­ный к вхо­ду уси­ли­те­ля. На ис­поль­зо­ва­нии по­ло­жи­тель­ной О. с. ос­но­ва­но дей­ст­вие бло­кинг-ге­не­ра­то­ров, муль­ти-виб­ра­то­ров, ге­не­ра­то­ров си­ну­сои­даль­ных ко­ле­ба­ний и др. В оп­ти­ке по­ло­жи­тель­ная О. с., осу­ще­ст­в­ляе­мая оп­тич. ре­зо­на­то­ром, ис­поль­зу­ет­ся для ге­не­ра­ции и уси­ле­ния из­лу­че­ния в ла­зе­рах, для внут­ри­ре­зо­на­тор­но­го пре­об­ра­зо­ва­ния час­то­ты, в т. ч. па­ра­мет­рич. ге­не­ра­ции све­та. При­ме­ром уст­ройств с от­ри­ца­тель­ной О. с. яв­ля­ют­ся разл. сис­те­мы ав­тома­тич. ре­гу­ли­ро­ва­ния. Так, ме­ха­нич. от­ри­ца­тель­ная О. с. осу­ще­ст­в­ля­ет­ся с по­мо­щью цен­тро­беж­но­го ре­гу­ля­то­ра Уат­та, при­ме­няе­мо­го для ста­би­ли­за­ции ско­ро­сти вра­ще­ния ва­ла па­ро­вой ма­ши­ны. Элек­трич. от­ри­ца­тель­ная О. с. ис­поль­зу­ет­ся в ста­би­ли­за­то­рах на­пря­же­ния и в сис­те­мах ав­то­ма­тич. ре­гу­ли­ро­ва­ния уси­ле­ния в ра­дио­при­ём­ни­ках.

О. с. на­зы­ва­ет­ся ли­ней­ной, ес­ли сиг­нал, воз­вра­щае­мый на вход сис­те­мы, из­ме­ня­ет­ся про­пор­цио­наль­но сиг­на­лу на её вы­хо­де $U_{вых}$, то­гда сиг­нал в це­пи О. с. ра­вен $βU_{вых}$, где $β$ – ко­эф. пе­ре­да­чи по ка­на­лу О. с. Ес­ли сиг­нал, воз­вра­щае­мый на вход сис­те­мы, из­ме­ня­ет­ся по бо­лее слож­но­му, не­ли­ней­но­му за­ко­ну, то О. с. на­зы­ва­ет­ся не­ли­ней­ной. В этом слу­чае сиг­нал в це­пи О. с. ха­рак­те­ри­зу­ет­ся не­ли­ней­ной пе­ре­да­точ­ной функ­ци­ей $f(U_{вых})$.

Тео­рия О. с. опи­сы­ва­ет по­ве­де­ние сис­тем с разл. за­ко­на­ми пре­об­ра­зо­ва­ния сиг­на­лов в бло­ках, изо­бра­жён­ных на рис. 1. Эти за­ко­ны мо­гут иметь ха­рак­тер ал­геб­ра­ич. дей­ст­вий, диф­фе­рен­ци­ро­ва­ния, ин­тег­ри­ро­ва­ния и т. п.

Ес­ли сиг­нал в це­пи О. с. воз­вра­ща­ет­ся на вход сис­те­мы мгно­вен­но, то О. с. на­зы­ва­ют бе­зы­нер­ци­он­ной. Од­на­ко ча­ще О. с. инер­ци­он­на, сиг­нал по це­пи О. с. по­сту­па­ет с не­ко­то­рой за­держ­кой. В ра­дио­элек­тро­ни­ке в этом слу­чае ис­поль­зу­ет­ся тер­мин «за­паз­ды­ваю­щая О. с.». Инер­ци­он­ность О. с. влия­ет на ско­рость из­ме­не­ния вы­ход­но­го сиг­на­ла.

В со­сре­до­то­чен­ных инер­ци­он­ных сис­те­мах О. с. осу­ще­ст­в­ля­ет­ся по­сред­ст­вом за­ви­си­мо­стей ско­ро­стей $dU_i/dt$ от зна­че­ний са­мих ве­ли­чин $U_i$, ха­рак­те­ри­зую­щих про­цесс в дан­ный мо­мент вре­ме­ни. Тео­ре­ти­че­ски та­кая связь опи­сы­ва­ет­ся сис­те­мой обык­но­вен­ных диф­фе­рен­ци­аль­ных урав­не­ний:

$$\frac{dU}{dt}=f_i(U_1, ..., U_n), i=1, \ldots, n,\tag{*}$$

где $f_i$ – не­ко­то­рые функ­ции, в об­щем слу­чае не­ли­ней­ные, $n$ – чис­ло сте­пе­ней сво­бо­ды сис­те­мы (раз­мер­ность фа­зо­во­го про­стран­ст­ва), $t$ – время. Тео­рия О. с. по­зво­ля­ет вы­де­лить ти­пич­ные, уни­вер­саль­ные эф­фек­ты са­мо­воз­дей­ст­вия сис­те­мы, со­стоя­щей из не­ко­то­ро­го ко­неч­но­го чис­ла под­сис­тем, ко­то­рые ока­зы­ва­ют вли­я­ние друг на дру­га. Важ­ней­шим эле­мен­том та­ко­го ана­ли­за яв­ля­ет­ся ис­сле­до­ва­ние би­фур­ка­ций ста­цио­нар­ных ре­ше­ний сис­те­мы уравнений (*) при из­ме­не­нии па­ра­мет­ров за­да­чи и со­от­вет­ст­вую­щих из­ме­не­ний фа­зо­во­го порт­ре­та сис­те­мы. Мн. про­цес­сы (взрыв, вос­пла­ме­не­ние, элек­трич. про­бой, фа­зо­вый пе­ре­ход 1-го ро­да и т. д.) яв­ля­ют­ся след­ст­ви­ем по­ло­жи­тель­ной О. с. в сис­те­ме (см. Тер­мо­ди­на­ми­ка не­рав­но­вес­ных про­цес­сов). В сис­те­ме с бис­та­биль­но­стью (на­ли­чи­ем двух ус­той­чи­вых ста­цио­нар­ных со­стоя­ний) воз­мож­ны скач­ко­об­раз­ные из­ме­не­ния со­стоя­ния при не­пре­рыв­ном из­ме­не­нии ко­эф. пе­ре­да­чи по ка­на­лу О. с. Бис­та­биль­ные сис­те­мы ве­дут се­бя по­доб­но сис­те­мам с фа­зо­вым пе­ре­хо­дом (см. Си­нер­ге­ти­ка). В ме­ха­нич. сис­те­мах при­ме­ром бис­та­биль­но­сти яв­ля­ет­ся скач­ко­об­раз­ное из­ме­не­ние про­ги­ба уп­ру­гой пла­стин­ки под дей­ст­ви­ем при­ло­жен­ной на­груз­ки. В оп­тич. сис­те­мах важ­ную роль иг­ра­ет оп­ти­че­ская би­ста­биль­ность ин­тен­сив­но­сти ко­ге­рент­но­го све­та в ре­зо­на­то­ре Фаб­ри – Пе­ро с на­сы­щаю­щим­ся по­гло­ти­те­лем.

Для сис­тем, опи­сы­вае­мых дву­мя урав­не­ния­ми (*), на фа­зо­вой плос­ко­сти, кро­ме осо­бых то­чек (со­стоя­ний рав­но­ве­сия), мо­гут так­же воз­ни­кать осо­бые тра­ек­то­рии – пре­дель­ные цик­лы, от­ве­чаю­щие ав­то­ко­ле­ба­ни­ям. Ав­то­ко­ле­ба­ния – об­щее свой­ст­во не­ли­ней­ных сис­тем с по­ло­жи­тель­ной О. с. Ко­ле­ба­ния в га­зо­вом раз­ря­де, вы­зы­ваю­щие мер­ца­ние не­оно­вой рек­ла­мы, и са­мо­про­из­воль­ное за­вы­ва­ние во­до­про­вод­ной тру­бы при от­кры­ва­нии кра­на, флат­тер са­мо­лё­тов и зву­ча­ние ду­хо­вых и смыч­ко­вых муз. ин­ст­ру­мен­тов оди­на­ко­во опи­сы­ва­ют­ся тео­ри­ей, раз­ли­ча­ют­ся лишь раз­ны­ми фи­зич. ме­ха­низ­ма­ми фор­ми­ро­ва­ния О. с. ме­ж­ду разл. сте­пе­ня­ми сво­бо­ды со­от­вет­ст­вую­щих сис­тем.

В био­ло­гич. сис­те­мах важ­ную роль иг­ра­ет О. с., от­вет­ст­вен­ная за воз­ник­но­ве­ние био­рит­мов и др. пе­рио­дич. про­цес­сов, напр. про­цес­сов ды­ха­ния жи­вых кле­ток (цикл Креб­са) и серд­це­бие­ния. В эко­ло­гич. сис­те­мах хо­ро­шо из­вест­ны пе­рио­дич. ко­ле­ба­ния чис­лен­но­сти по­пуля­ций в со­об­ще­ст­вах ти­па «хищ­ник–жерт­ва». О. с. здесь осу­ще­ст­в­ля­ет­ся за счёт уве­ли­че­ния (умень­ше­ния) ско­ро­сти при­рос­та чис­лен­но­сти хищ­ни­ков при уве­ли­че­нии (умень­ше­нии) чис­ла жертв, яв­ляю­щих­ся для них пи­щей (мо­дель Лот­ки – Воль­тер­ры). Из­вест­ны окис­ли­тель­но-вос­ста­но­ви­тель­ные ко­ле­ба­тель­ные ре­ак­ции, про­те­каю­щие в при­сут­ст­вии ка­та­ли­за­то­ра (ре­ак­ции Бе­ло­усо­ва – Жа­бо­тин­ско­го), в ко­то­рых цвет и кон­цен­тра­ция реа­ген­тов из­ме­ня­ют­ся пе­рио­ди­че­ски.

С рос­том чис­ла сте­пе­ней сво­бо­ды ус­лож­не­ние ди­на­ми­ки сис­те­мы, напр. при из­ме­не­нии ко­эф. пе­ре­да­чи по ка­на­лу О. с., мо­жет осу­ще­ст­в­лять­ся за счёт би­фур­ка­ции пе­рио­дич. дви­же­ний, при­во­дя­щих, в ча­ст­но­сти, к ро­ж­де­нию стран­но­го ат­трак­то­ра. По­ве­де­ние фа­зо­вых тра­ек­то­рий на та­ком ат­трак­то­ре хао­тич­но, по­это­му с ро­ж­де­ни­ем стран­но­го ат­трак­то­ра свя­зы­ва­ют воз­ник­но­ве­ние в сис­те­мах хао­тич. дви­же­ния (см. Сто­хас­ти­че­ские ко­ле­ба­ния). Та­кое хао­тич. дви­же­ние мо­жет де­мон­ст­ри­ро­вать сис­те­ма, опи­сы­вае­мая все­го тре­мя урав­не­ния­ми ти­па (*).

О. с. в сис­те­мах с рас­пре­де­лён­ны­ми па­ра­мет­ра­ми но­сит не­ло­каль­ный ха­рак­тер, т. е. взаи­мо­влия­ние осу­ще­ст­в­ля­ет­ся ме­ж­ду ве­ли­чи­на­ми, рас­по­ло­жен­ны­ми в разл. точ­ках про­стран­ст­ва. Во мно­гих фи­зич. и хи­мич. сис­те­мах та­кое взаи­мо­влия­ние обу­слов­ле­но про­цес­са­ми не­об­ра­ти­мо­го пе­ре­но­са ти­па диф­фу­зии. На­ли­чие О. с. ме­ж­ду по­то­ка­ми вбли­зи по­ло­же­ний рав­но­ве­сия в тер­мо­ди­на­ми­ке впер­вые от­ме­че­но Л. Он­са­ге­ром (см. Он­са­ге­ра тео­ре­ма). На язы­ке тео­рии не­ли­ней­ных волн та­кая О. с. при­во­дит к эф­фек­там син­хро­ни­за­ции и кон­ку­рен­ции мод, что, в свою оче­редь, вле­чёт за со­бой разл. яв­ле­ния са­мо­ор­га­ни­за­ции.

В оп­ти­ке са­мо­воз­дей­ст­вие све­та при­во­дит к разл. эф­фек­там ге­не­ра­ции гар­мо­ник, вы­ну­ж­ден­но­му рас­сея­нию све­та и др. Макс. ко­эф. пе­ре­да­чи по ка­на­лу по­ло­жи­тель­ной О. с. в этих слу­ча­ях обес­пе­чи­ва­ет­ся при вы­пол­не­нии ус­ло­вий ре­зо­нанс­ной свя­зи мод (фа­зо­во­го син­хро­низ­ма).

При­чин­но-след­ст­вен­ная связь, об­ус­лов­лен­ная О. с. в разл. сис­те­мах, изу­ча­ет­ся во мно­гих дис­ци­п­ли­нах. Так, О. с. иг­ра­ет клю­че­вую роль в разл. сис­те­мах ис­кус­ст­вен­но­го ин­тел­лек­та в ин­фор­ма­ти­ке. В жи­вых клет­ках на прин­ци­пе от­ри­ца­тель­ной О. с. ос­но­ва­ны мн. ме­ха­низ­мы ре­гу­ля­ции ра­бо­ты ге­нов и фер­мен­тов. Бес­чис­лен­ные при­ме­ры воз­дей­ст­вия разл. О. с. мож­но на­блю­дать в эко­но­ми­ке, социо­ло­гии и обы­ден­ной че­ло­ве­че­ской жиз­ни.

В теории и технике управления

О. с. яв­ля­ет­ся важ­ней­шим прин­ци­пом при­ня­тия ре­ше­ний (вы­ра­бот­ки управ­ляю­щих воз­дей­ст­вий) при управ­ле­нии объ­ек­та­ми разл. при­ро­ды: тех­нич., эко­но­мич., ор­га­ни­за­ци­он­ны­ми и др. Гл. дос­то­ин­ст­во О. с. – обес­пе­че­ние не­пре­рыв­ной кор­рек­ции управ­ляю­щих воз­дей­ст­вий по­сред­ст­вом срав­не­ния вы­ход­ных ре­зуль­та­тов с за­дан­ны­ми (же­лае­мы­ми). В осн. ис­поль­зу­ют сис­те­мы с от­ри­ца­тель­ной О. с. В та­ко­го ро­да сис­те­мах (рис. 2) пла­ни­ру­ет­ся (про­грам­ми­ру­ет­ся) бу­ду­щее же­лае­мое со­стоя­ние вы­хо­да. 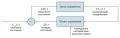За­тем пу­тём на­хо­ж­де­ния раз­но­сти ме­ж­ду пла­ни­руе­мым $S_{пл}(t)$ и фак­ти­че­ским $S(t)$ со­стоя­ния­ми оп­ре­де­ля­ет­ся из­ме­не­ние со­стоя­ния сис­те­мы $ΔS(t)=S_{пл}(t)-S(t)$ и вы­ра­баты­ва­ет­ся не­об­хо­ди­мое управ­ляю­щее воз­дей­ст­вие $U(t+1)$, при­зван­ное све­сти к ми­ни­му­му рас­со­гла­со­ва­ние ме­ж­ду тре­буе­мым и фак­ти­че­ским со­стоя­ния­ми сис­те­мы.

По ви­ду опе­ра­то­ра свя­зи вы­ход­ной ве­ли­чи­ны объ­ек­та с вход­ной раз­ли­ча­ют жё­ст­кую и гиб­кую О. с. В пер­вой опе­ра­тор свя­зи – ко­эф. про­пор­цио­наль­но­сти. Во вто­рой до­пол­ни­тель­но вклю­ча­ет­ся связь по про­из­вод­ной (ско­ро­сти из­ме­не­ния) вы­ход­ной ве­ли­чи­ны, что по­вы­ша­ет ус­той­чи­вость сис­те­мы. Ес­ли ма­те­ма­тич. мо­дель свя­зей ве­ли­чин в объ­ек­те из­вест­на, вид и зна­че­ния па­ра­мет­ров опе­ра­то­ра О. с. оп­ре­де­ля­ют­ся рас­чёт­ны­ми ме­то­да­ми. Ес­ли мо­дель объ­ек­та не­из­вест­на, то при­бе­га­ют к ме­то­дам иден­ти­фи­ка­ции мо­де­ли на ос­но­ве ин­фор­ма­ции, по­лу­чае­мой в про­цес­се функ­цио­ни­ро­ва­ния сис­те­мы «объ­ект – управ­ляю­щая сис­те­ма» и по­сле­дую­щей на­строй­ке кон­ту­ра О. с. В сис­те­мах с мно­го­звен­ны­ми объ­ек­та­ми для по­вы­ше­ния ка­че­ст­ва управ­ле­ния О. с. ох­ва­ты­ва­ют не толь­ко объ­ект в це­лом, но и его отд. зве­нья.