ГОДО́ГРАФ

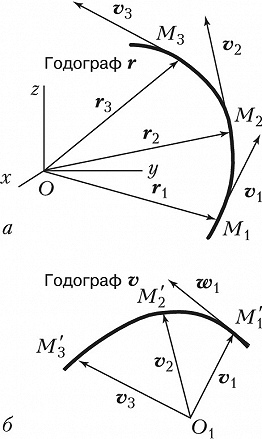
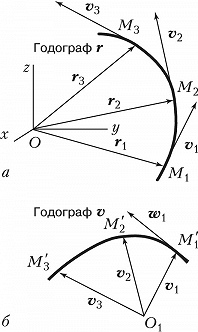
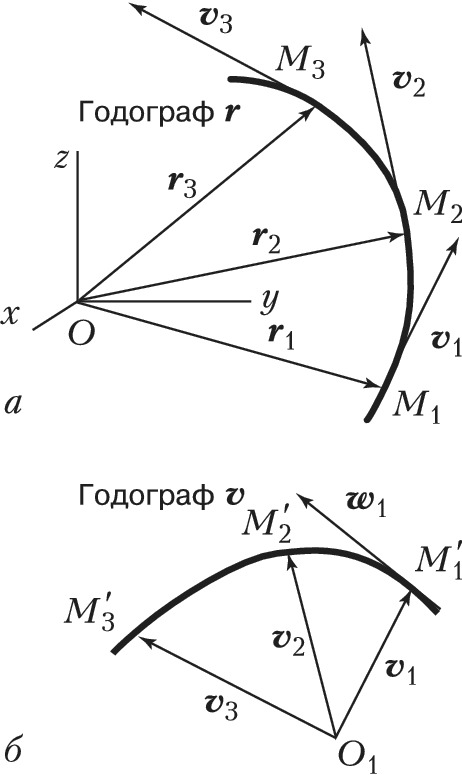
ГОДО́ГРАФ в ме­ха­ни­ке (от греч. ὁδός – путь, дви­же­ние, на­прав­ле­ние и ...граф), кри­вая, яв­ляю­щая­ся гео­мет­рич. ме­стом кон­цов пе­ре­мен­но­го век­то­ра (век­тор-функ­ции), зна­че­ния ко­то­ро­го при раз­ных зна­че­ни­ях ар­гу­мен­та от­ло­же­ны от не­ко­то­ро­го об­ще­го на­ча­ла. Ес­ли, напр., по­ло­же­ние дви­жу­щей­ся точ­ки оп­ре­де­лять её ра­ди­ус-век­то­ром $\boldsymbol r$, про­во­ди­мым из на­ча­ла от­счё­та $O$, то Г. век­то­ра $\boldsymbol r$ да­ёт тра­ек­то­рию точ­ки (рис., а). Оп­ре­де­лив зна­че­ния век­то­ра ско­ро­сти $\boldsymbol v$ точ­ки в раз­ные мо­мен­ты вре­ме­ни и от­ло­жив эти век­то­ры от об­ще­го на­ча­ла $O_1$, по­лу­ча­ют Г. век­то­ра ско­ро­сти (рис., б) и т. д.

Про­из­вод­ная от пе­ре­мен­но­го век­то­ра $\boldsymbol {u}(t)$ по ар­гу­мен­ту $t$ да­ёт век­тор, на­прав­ле­ние ко­то­ро­го сов­па­да­ет с на­прав­ле­ни­ем ка­са­тель­ной к Г. век­то­ра $\boldsymbol{u}(t)$ в со­от­вет­ст­вую­щей точ­ке. Так, на­прав­ле­ние век­то­ра ско­ро­сти точ­ки в по­ло­же­нии $M_1$, рав­но­го $\boldsymbol {v}_1=(d\boldsymbol{r}/dt)_1$, сов­па­да­ет с на­прав­ле­ни­ем ка­са­тель­ной к Г. век­то­ра $\boldsymbol r$ в этой точ­ке; на­прав­ле­ние век­то­ра ус­ко­ре­ния точ­ки в по­ло­же­нии $M_1$, рав­но­го $\boldsymbol {w}_1=(d\boldsymbol{v}/dt)_1$, сов­па­да­ет с на­прав­ле­ни­ем ка­са­тель­ной к Г. век­то­ра $\boldsymbol v$ в точ­ке .