НЕСЖИМА́ЕМАЯ ЖИ́ДКОСТЬ

НЕСЖИМА́ЕМАЯ ЖИ́ДКОСТЬ, мо­дель­ный объ­ект ме­ха­ни­ки сплош­ной сре­ды, те­ку­чая сре­да, про­из­воль­но вы­бран­ный объ­ём ко­то­рой [т. н. ла­гран­жев объ­ём, со­стоя­щий из од­но­го и то­го же на­бо­ра жид­ких час­тиц (т. е. ма­лых объ­ё­мов жид­ко­сти)] ос­та­ёт­ся не­из­мен­ным во всё вре­мя дви­же­ния. Т. о., плот­ность $ρ$ в час­ти­це Н. ж. ос­та­ёт­ся по­сто­ян­ной:$$\frac{d\rho}{dt}=\frac{\partial \rho}{\partial x}+v \cdot V_\rho=0,$$где $t$ – вре­мя, $v$ – век­тор ско­ро­сти сре­ды. В од­но­род­ной Н. ж. плот­ность не за­ви­сит от про­стран­ст­вен­ных ко­ор­ди­нат и слу­жит фи­зич. ха­рак­те­ри­сти­кой дан­ной жид­ко­сти; в не­од­но­род­ной Н. ж. плот­ность ос­та­ёт­ся по­сто­ян­ной в пре­де­лах жид­кой час­ти­цы.

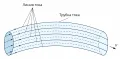
Урав­не­ние не­раз­рыв­но­сти для Н. ж. име­ет вид: div $v=0$. Вдоль труб­ки то­ка Н. ж. спра­вед­ли­во урав­не­ние $Sv_{ср}=$ const, где $S$ – пло­щадь по­пе­реч­но­го се­че­ния труб­ки то­ка в дан­ной точ­ке (для не­ус­та­но­вив­ше­го­ся те­че­ния – в дан­ный мо­мент вре­ме­ни), $v_{ср}$ – ср. ско­рость те­че­ния в труб­ке. Т. о., ско­рость те­че­ния в труб­ке то­ка об­рат­но про­пор­цио­наль­на её по­пе­реч­но­му се­че­нию.

Мо­дель Н. ж. в боль­шин­ст­ве слу­ча­ев при­бли­жён­но при­ме­ни­ма к лю­бой жид­ко­сти. Од­на­ко в не­ко­то­рых слу­ча­ях сле­ду­ет учи­ты­вать сжи­мае­мость жид­ко­сти (напр., при боль­шом гид­ро­ста­тич. дав­ле­нии или при изу­че­нии рас­про­стра­не­ния зву­ка в жид­ко­сти). Так, при дав­ле­нии ок. 1000 атм (10⁸ Па) сжа­тие во­ды дос­ти­га­ет 5% пер­во­на­чаль­но­го объ­ё­ма; в этом слу­чае мо­дель Н. ж. не­при­ме­ни­ма.