ЛИССАЖУ́ ФИГУ́РЫ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
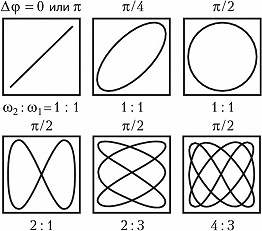
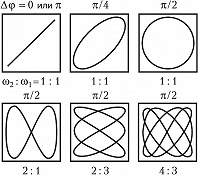
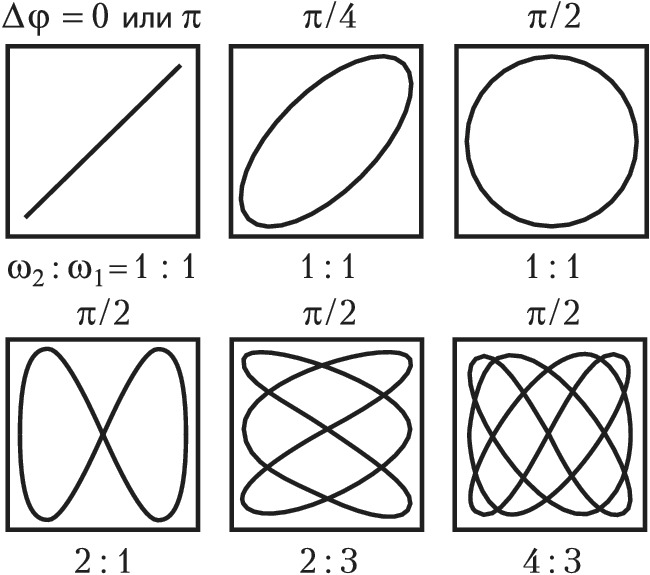
ЛИССАЖУ́ ФИГУ́РЫ, замкнутые плоские кривые, описываемые точкой, движение которой является суперпозицией двух взаимно перпендикулярных колебаний с отношением частот, равным рациональному числу. Впервые были подробно изучены франц. математиком Ж. А. Лиссажу в 1857–58. Л. ф. описываются системой параметрич. уравнений (параметр – время $t$)$$x=A_1\text{cos}(ω_1t+φ_1), \;y=A_2\text{cos}(ω_2t+φ_2)$$при отношении частот $ω_2:ω_1$, равном рациональному числу. Л. ф. вписаны в прямоугольник со сторонами $2A_1$ и $2A_2$, параллельными соответственно осям $x$ и $y$. Вид Л. ф. зависит от отношения частот $ω_2:ω_1$ и разности фаз $Δφ=φ_2-φ_1$ обоих колебаний. В случае равных частот $(ω_2:ω_1=1:1)$ Л. ф. представляют собой эллипсы, которые при $Δφ=0$ или $\pmπ$ вырождаются в отрезки прямых, а при $Δφ=\pmπ/2$ и $A_1=A_2$ превращаются в окружность (рис.). При неравных частотах Л. ф. имеют более сложный вид. Отношение числа касаний Л. ф. горизонтальной и вертикальной сторон прямоугольника, в который она вписана, даёт отношение частот $ω_2:ω_1$. Направление движения точки по Л. ф. определяется разностью фаз $Δφ$.
Л. ф. можно наблюдать, напр., на экране осциллографа, подав на его вертикально и горизонтально отклоняющие пластины переменные напряжения с отношением частот, равным рациональному числу. Вид Л. ф. позволяет определить соотношения между частотами и фазами напряжений. При небольшом отклонении отношения частот от рационального числа наблюдается медленное изменение разности фаз во времени и плавное изменение вида фигур Лиссажу.