КВА́НТОВАЯ ХРОМОДИНА́МИКА

КВА́НТОВАЯ ХРОМОДИНА́МИКА (КХД), кван­то­вая тео­рия силь­но­го взаи­мо­дей­ст­вия цвет­ных глю­он­ных и квар­ко­вых по­лей, по­стро­ен­ная на ос­но­ве прин­ци­па ло­каль­ной ка­либ­ро­воч­ной ин­ва­ри­ант­но­сти (ка­либ­ро­воч­ной сим­мет­рии) от­но­си­тель­но пре­об­ра­зо­ва­ний в трёх­мер­ном ком­плекс­ном про­стран­ст­ве внутр. сим­мет­рий. По совр. пред­став­ле­ни­ям, КХД со­став­ля­ет ос­но­ву опи­са­ния силь­но­го взаи­мо­дей­ст­вия ме­ж­ду ад­ро­на­ми и от­ве­ча­ет за си­лы, свя­зы­ваю­щие квар­ки в ад­ро­ны.

КХД воз­ник­ла в нач. 1970-х гг. в ре­зуль­та­те син­те­за пред­став­ле­ния о цве­те квар­ков, пар­тон­ной мо­де­ли глу­бо­ко не­уп­ру­го­го взаи­мо­дей­ст­вия (см. Пар­то­ны) и ма­те­ма­тич. ап­па­ра­та не­абе­ле­вых ка­либ­ро­воч­ных по­лей.

Квар­ко­вая мо­дель, со­глас­но ко­то­рой все ад­ро­ны яв­ля­ют­ся свя­зан­ны­ми со­стоя­ния­ми ли­бо па­ры кварк-ан­тик­варк (ме­зо­ны), ли­бо трёх квар­ков (ба­рио­ны), хо­ро­шо объ­яс­ня­ла сис­те­ма­ти­ку ад­ро­нов, т. е. их груп­пи­ров­ку по свой­ст­вам в уни­тар­ные и изо­то­пич. муль­ти­пле­ты, рас­ще­п­ле­ние по мас­сам внут­ри этих муль­ти­пле­тов, а так­же не­ко­то­рые ста­тич. свой­ст­ва ад­ро­нов (напр., от­но­ше­ния ве­ли­чин маг­нит­ных мо­мен­тов). Важ­ный со­став­ной эле­мент этой мо­де­ли – пред­по­ло­же­ние о су­ще­ст­во­ва­нии до­пол­нит. ха­рак­те­ри­сти­ки квар­ков – т. н. цве­та, вве­де­ние ко­то­ро­го бы­ло вы­зва­но не­об­хо­ди­мо­стью ут­рое­ния чис­ла квар­ков каж­до­го ти­па (аро­ма­та), для то­го что­бы, не вхо­дя в про­ти­во­ре­чие с прин­ци­пом Пау­ли, мож­но бы­ло объ­яс­нить су­ще­ст­во­ва­ние та­ких ба­рио­нов, как, напр., $\Delta^{++}$, со­стоя­щих из трёх $u$-квар­ков с оди­на­ко­вым на­прав­ле­ни­ем спи­на. При этом ре­аль­но на­блю­дае­мые ад­ро­ны «бес­цвет­ны». От­сут­ст­вие в при­ро­де ме­зо­нов с дву­мя квар­ка­ми, а так­же ве­ли­чи́­ны ве­ро­ят­но­сти рас­па­да $\pi^0$-ме­зо­на на два фо­то­на $(\pi^0 \to 2\gamma)$ и се­че­ния ан­ни­ги­ля­ции элек­трон-по­зи­трон­ной па­ры в ад­ро­ны ($e^+e^- \to$ ад­ро­ны) од­но­знач­но ука­зы­ва­ли на сим­мет­рию от­но­си­тель­но пре­об­ра­зо­ва­ний в трёх­мер­ном цве­то­вом про­стран­ст­ве, со­от­вет­ст­вую­щую груп­пе сим­мет­рий SU (3).

Рис. 1. Аннигиляция электрон-позитронной пары в две адронные струи в кварковой модели адронов.

Пред­став­ле­ние о пар­то­нах воз­ник­ло в ре­зуль­та­те экс­пе­ри­мен­таль­но об­на­ру­жен­но­го раз­ли­чия в по­ве­де­нии струк­тур­ных функ­ций глу­бо­ко не­уп­ру­гих про­цес­сов и форм­фак­то­ров уп­ру­го­го рас­сея­ния леп­то­нов на ад­ро­нах, ко­то­рые ока­за­лось воз­мож­ным со­вмес­тить толь­ко на ос­но­ве пред­по­ло­же­ния о су­ще­ст­во­ва­нии внут­ри про­то­на то­чеч­ных (сла­бо­взаи­мо­дей­ст­вую­щих) со­став­ляю­щих ад­ро­нов – пар­то­нов. Даль­ней­шее экс­пе­рим. изу­че­ние жё­ст­ких про­цес­сов (т. е. про­цес­сов с боль­шой пе­ре­да­чей им­пуль­са), в ко­то­рых ис­сле­до­ва­лась струк­ту­ра ад­ро­на на ма­лых рас­стоя­ни­ях, по­ка­за­ло, что за­ря­жен­ные пар­то­ны то­ж­де­ст­вен­ны квар­кам и ан­тик­вар­кам. Т. о., по­лу­ча­лось, что, с од­ной сто­ро­ны, на рас­стоя­нии по­ряд­ка ра­диу­са ад­ро­на (по­ряд­ка 10^–13 см) квар­ки долж­ны дос­та­точ­но силь­но взаи­мо­дей­ст­во­вать, что­бы об­ра­зо­вы­вать та­кие проч­ные сис­те­мы, как ад­ро­ны, а с дру­гой – эф­фек­тив­ная кон­стан­та это­го взаи­мо­дей­ст­вия долж­на ос­ла­бе­вать на рас­стоя­ни­ях по­ряд­ка 0,1 ра­диу­са ад­ро­на. 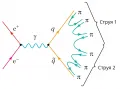Ос­лаб­ле­ние эф­фек­тив­ной кон­с­тан­ты взаи­мо­дей­ст­вия квар­ков с умень­ше­ни­ем рас­стоя­ния бы­ло позд­нее на­зва­но асим­пто­ти­че­ской сво­бо­дой. Воз­рас­та­ние же кон­стан­ты взаи­мо­дей­ст­вия с рос­том рас­стоя­ния да­ва­ло воз­мож­ность объ­яс­нить яв­ле­ние «не­вы­ле­та­ния» квар­ков (кон­файн­мент), про­яв­ляю­щее­ся в не­на­блю­дае­мо­сти сво­бод­ных квар­ков. Напр., в про­цес­се ан­ни­ги­ля­ции элек­тро­на $(e^-)$ и по­зи­тро­на $(e^+)$ (рис. 1) обра­зу­ют­ся раз­ле­таю­щие­ся кварк $(q)$ и ан­тик­варк $(\tilde q)$, рост взаи­мо­дей­ст­вия меж­ду ко­то­ры­ми при­во­дит к ро­ж­де­нию из ва­куу­ма пар кварк-ан­тик­варк ($\pi$-ме­зон) и «обес­цве­чи­ва­нию» раз­ле­таю­щих­ся квар­ка и ан­тик­вар­ка и рож­дён­ных квар­ков и ан­ти­квар­ков и пре­вра­ще­нию их в ад­ро­ны. В ре­зуль­та­те вме­сто $q$ и $\tilde q$ на­блю­да­ют­ся две ад­рон­ные струи, ле­тя­щие в про­ти­во­по­лож­ные сто­ро­ны.

Ре­шаю­щим ша­гом для соз­да­ния КХД бы­ло ус­та­нов­ле­ние свой­ст­ва ос­лаб­ле­ния взаи­мо­дей­ст­вия с умень­ше­ни­ем рас­стоя­ния для клас­са ка­либ­ро­воч­ных по­лей, ос­но­ван­ных на не­абе­ле­вых груп­пах сим­мет­рии, к ко­то­рым от­но­сит­ся и груп­па SU (3).

Ос­но­ву КХД об­ра­зу­ют три цвет­ных со­стоя­ния квар­ко­во­го по­ля Ди­ра­ка $q^\alpha(x)$ ($x$ – точ­ка про­стран­ст­ва-вре­ме­ни, $\alpha=1,2,3$ – цве­то­вой ин­декс) ка­ж­до­го аро­ма­та (u,d,s,с,b,t), пре­об­ра­зую­щих­ся друг че­рез дру­га при пре­об­ра­зо­ва­ни­ях в цве­то­вом про­стран­ст­ве. Кван­та­ми по­лей яв­ля­ют­ся цвет­ные квар­ки. По сво­ей струк­ту­ре КХД ана­ло­гич­на кван­то­вой элек­тро­ди­на­ми­ке (КЭД), но име­ет су­ще­ст­вен­ные от­ли­чия. В КЭД элек­т­рич. за­ряд вслед­ст­вие ка­либ­ро­воч­ной сим­мет­рии по­ро­ж­да­ет элек­тро­маг­нит­ное по­ле, а в КХД цвет­ные квар­ки по­ро­ж­да­ют во­семь раз­но­вид­но­стей цве­то­вых глю­он­ных по­лей – век­тор­ных ка­либ­ро­воч­ных Ян­га – Мил­лса по­лей. По­сколь­ку глю­он­ные по­ля, в от­ли­чие от элек­тро­маг­нит­но­го, не­сут цве­то­вой за­ряд, они са­ми по­ро­ж­да­ют глю­он­ные по­ля и взаи­мо­дей­ст­ву­ют друг с дру­гом. Вслед­ст­вие это­го урав­не­ния для глю­он­ных по­лей (в от­ли­чие от урав­не­ний Мак­с­вел­ла для ва­куу­ма) не­ли­ней­ны. Кван­та­ми глю­он­но­го по­ля яв­ля­ют­ся во­семь глюо­нов (ана­ло­ги фо­то­на в КЭД), имею­щих ну­ле­вую мас­су по­коя и спин 1. При ис­пус­ка­нии и по­гло­ще­нии глюо­нов квар­ки (и глюо­ны) мо­гут ме­нять свой цвет, но со­хра­ня­ют тип (аро­мат).

Квантование и диаграммы Фейнмана

Рис. 2. Вершины диаграмм Фейнмана в квантовой хромодинамике. Сплошные линии изображают кварки, спиральные – глюоны.

По­сле­до­ва­тель­ной схе­мы кван­то­ва­ния в КХД по­ка нет. Обыч­но ис­поль­зуе­мое кван­то­ва­ние квар­ко­вых и глю­он­ных по­лей про­во­дит­ся для сво­бод­ных, не взаи­мо­дей­ст­вую­щих по­лей, и в этом оно фор­маль­но не от­ли­ча­ет­ся от кван­то­ва­ния в КЭД. Од­на­ко та­кая опе­ра­ция в КХД не впол­не за­кон­на из-за от­сут­ствия сво­бод­ных квар­ков и глюо­нов. Учёт же взаи­мо­дей­ст­вия про­во­дит­ся с по­мо­щью тео­рии воз­му­ще­ний, изо­бра­жае­мой диа­грам­ма­ми Фейн­ма­на, ко­гда ка­ж­дый кварк или глю­он мо­жет ис­пус­тить (или по­гло­тить) глю­он, а глю­он мо­жет ис­пус­тить (или по­гло­тить) па­ру глюо­нов. В КХД, в от­ли­чие от КЭД, в диа­грам­мах Фейн­ма­на воз­мож­ны не толь­ко кварк-глю­он­ные вер­ши­ны (рис. 2,а), но и трёх­глю­он­ные (рис. 2,б), и че­ты­рёх­глю­он­ные (рис. 2,в).

Пра­ви­ла Фейн­ма­на диа­грамм по­зво­ля­ют вы­чис­лять лю­бые про­цес­сы с учас­ти­ем квар­ков и глюо­нов. Од­на­ко, как и в КЭД, ин­те­гра­лы по им­пуль­сам про­ме­жу­точ­ных (вир­ту­аль­ных) час­тиц ока­зы­ва­ют­ся бес­ко­неч­ны­ми, рас­хо­дя­щи­ми­ся при боль­ших или ма­лых им­пуль­сах (УФ- и ИК-рас­хо­ди­мо­сти). Что­бы из­бе­жать ИК-рас­хо­ди­мо­стей, при рас­чё­тах про­цес­сов с уча­сти­ем ад­ро­нов все­гда рас­смат­ри­ва­ют кварк-глю­он­ные (пар­тон­ные) под­про­цес­сы, про­ис­хо­дя­щие на ма­лых рас­стоя­ни­ях (мень­ших раз­ме­ра ад­ро­нов), т. е. к.-л. об­ра­зом ре­гу­ля­ри­зо­ван­ные (напр., об­ре­зан­ные) в об­лас­ти ма­лых им­пуль­сов. (В КЭД по­доб­ные рас­хо­ди­мо­сти со­кра­ща­ют­ся при учё­те из­лу­че­ния мяг­ких фо­то­нов.) За­ви­си­мость се­че­ний под­про­цес­са от па­ра­мет­ра ИК-ре­гу­ля­ри­за­ции вы­де­ля­ет­ся в ви­де со­мно­жи­те­лей и вклю­ча­ет­ся в вол­но­вые или струк­тур­ные функ­ции ад­ро­нов, рас­смат­ри­вае­мые как фе­но­ме­но­ло­ги­че­ские (не­вы­чис­ляе­мые) эле­мен­ты схе­мы.

УФ-рас­хо­ди­мо­сти уст­ра­ня­ют, при­ме­няя стан­дарт­ные спо­со­бы ре­гу­ля­ри­за­ции (обыч­но об­ре­за­ние) и пе­ре­нор­ми­ров­ки в кван­то­вой тео­рии по­ля. Для мат­рич­ных эле­мен­тов мат­ри­цы пе­ре­хо­да все бес­ко­неч­ные мно­жи­те­ли по­сле пе­ре­нор­ми­ров­ки век­то­ров со­стоя­ний квар­ка и глюо­на со­би­ра­ют­ся в эф­фек­тив­ную (то­ко­вую) мас­су квар­ка $m_f(\mu^2)$ и эф­фек­тив­ную констан­ту взаи­мо­дей­ст­вия $g^2_\mu(\mu^2)$, где $\mu^2$ – не­ко­то­рый па­ра­метр (имею­щий раз­мер­ность квад­ра­та им­пуль­са), по­явив­ший­ся в ре­зуль­та­те ре­гу­ля­ри­за­ции. Ха­рак­тер­ной чер­той пе­ре­нор­ми­ро­воч­ной про­це­ду­ры в КХД яв­ля­ет­ся за­ви­си­мость эф­фек­тив­ной мас­сы и кон­стан­ты взаи­мо­дей­ст­вия от $\mu^2$. Она свя­за­на с тем, что квар­ки как сво­бод­ные час­ти­цы не на­блю­да­ют­ся.

Ренормализационная группа и асимптотическая свобода

Осо­бую роль в КХД иг­ра­ет ре­нор­ма­ли­за­ци­он­ная груп­па (ре­норм­груп­па), пред­став­ляю­щая со­бой груп­пу пре­об­ра­зо­ва­ний с из­ме­не­ни­ем зна­че­ний па­ра­мет­ра нор­ми­ров­ки и од­но­вре­мен­ным из­ме­не­ни­ем $g^2_{\mu}$. Это свя­за­но с тем, что кон­стан­та взаи­мо­дей­ст­вия ока­зы­ва­ет­ся не очень ма­лой, а чле­ны ря­да $[g^2_\mu \text{ln}(Q^2/ \mu^2)]^n$ [где $n=1,2,\dots$; $Q^2$ – квад­рат ха­рак­тер­ной пе­ре­да­чи че­ты­рёх­мер­но­го им­пуль­са (4-им­пуль­са)], воз­ни­каю­щие при вы­чис­ле­ни­ях по тео­рии воз­му­ще­ний, – дос­та­точ­но боль­ши­ми и тре­бу­ют сум­ми­ро­ва­ния, ко­то­рое удоб­но вы­пол­нять с по­мо­щью ап­па­ра­та ре­норм­груп­пы. Ин­ва­ри­ант­ный за­ряд ре­норм­груп­пы $g^2[Q^2, \mu^2, g^2_\mu]$, ко­то­рый не за­ви­сит от вы­бо­ра па­ра­мет­ра нор­ми­ров­ки $\mu^2$, оп­ре­де­ля­ет эф­фек­тив­ную кон­с­тан­ту взаи­мо­дей­ст­вия при квад­ра­те пе­ре­дан­но­го 4-им­пуль­са $Q^2$ или на рас­стоя­нии по­ряд­ка $1Q$ (в сис­те­ме еди­ниц $\hbar=c=1$; здесь $\hbar$  – по­сто­ян­ная План­ка, $c$ – ско­рость све­та).

Рис. 3. Зависимость αs от Q. Результаты разных экспериментов обозначены различными значками.

Сум­ми­ро­ва­ние «стар­ших» чле­нов в ин­ва­ри­ант­ном за­ря­де при­во­дит к эф­фек­тив­но­му за­ря­ду $\alpha_s$: $$\alpha_s(Q^2)=g^2[Q^2, \mu^2, g^2_\mu]/(4\pi)=12\pi/[11n_c-2n_f)\text{ln}(Q^2/\Lambda^2)],\quad\tag{1}$$где $n_c=3$ – чис­ло цве­тов, $n_f$ – чис­ло арома­тов. В от­ли­чие от КЭД $(n_c=0)$, где эф­фек­тив­ный за­ряд рас­тёт с рос­том $Q^2$, в КХД он умень­ша­ет­ся (ес­ли чис­ло аро­ма­тов $n_f<17$), т. е. с умень­ше­ни­ем рас­стоя­ния (рос­том $Q^2$) эф­фек­тив­ное взаи­мо­дей­ст­вие умень­ша­ет­ся (рис. 3), объ­ект ста­но­вит­ся асим­пто­ти­че­ски сво­бод­ным (не­взаи­мо­дей­ст­вую­щим). Это яв­ле­ние ан­ти­эк­ра­ни­ров­ки за­ря­да из-за по­ля­ри­за­ции ва­куу­ма в не­абе­ле­вых ка­либ­ро­воч­ных тео­ри­ях по­ля бы­ло об­на­ру­же­но в 1973 Д. По­лит­це­ром, а так­же Д. Грос­сом и Ф. Вил­че­ком (Но­бе­лев­ская пр., 2004) и яв­ля­ет­ся важ­ней­шим свой­ст­вом КХД. Оно по­зво­ля­ет ис­поль­зо­вать ап­па­рат тео­рии воз­му­ще­ний и рас­счи­ты­вать ха­рак­те­ри­сти­ки ад­рон­ных про­цес­сов, свя­зан­ные с взаи­мо­дей­ст­ви­ем квар­ков и глюо­нов на ма­лых рас­стоя­ни­ях.

По­след­нее вы­ра­же­ние в (1) пред­став­ля­ет со­бой ре­нормин­ва­ри­ант­ное, т. е. не за­ви­ся­щее от точ­ки нор­ми­ров­ки, вы­ра­же­ние для эф­фек­тив­но­го за­ря­да че­рез фун­дам. по­сто­ян­ную $\Lambda$, имею­щую раз­мер­ность им­пуль­са. В этом за­клю­ча­ет­ся ещё од­на осо­бен­ность КХД – фун­дам. раз­мер­ная по­сто­ян­ная по­яв­ля­ет­ся в тео­рии, со­дер­жа­щей без­раз­мер­ную кон­стан­ту взаи­мо­дей­ст­вия. Это яв­ле­ние бы­ло на­зва­но раз­мер­ной транс­му­та­ци­ей. Оно свя­за­но с тем, что в КХД из-за удер­жа­ния цве­та не­воз­мож­но соз­дать ста­тич. глю­он­ные по­ля и по­это­му нель­зя оп­ре­де­лить от­но­ше­ние за­ря­да к мас­се. Чи­с­ло­вое зна­че­ние $\Lambda$ в разл. схе­мах ре­гу­ляри­за­ции бу­дет раз­ным; в наи­бо­лее рас­про­стра­нён­ной схе­ме т. н. усе­чён­ной раз­мер­ной ре­гу­ля­ри­за­ции её экс­пе­рим. ве­ли­чи­на (в сис­те­ме $\hbar=c=1$) рав­на: $\Lambda$=210±30 МэВ. Эф­фек­тив­ный за­ряд при $Q^2=\Lambda^2$ фор­маль­но ста­но­вит­ся бес­ко­неч­ным, хо­тя уже раз­ра­бо­та­ны ме­то­ды уда­ле­ния этой бес­ко­неч­но­сти. Од­на­ко го­раз­до рань­ше (при $Q \leq 10\Lambda$) при­бли­же­ние стар­ших ло­га­риф­мов, на ос­но­ве ко­то­ро­го бы­ло по­лу­че­но вы­ра­же­ние (1), ока­зы­ва­ет­ся не­дос­та­точ­ным.

Су­ще­ст­ву­ет пред­по­ло­же­ние, что рост эф­фек­тив­но­го за­ря­да при уве­ли­че­нии рас­стоя­ния мож­но свя­зать с яв­ле­ни­ем удер­жа­ния цве­та, пре­пят­ст­вую­щим вы­би­ва­нию квар­ков и глюо­нов из ад­ро­на, од­на­ко к.-л. стро­го­го до­ка­за­тель­ст­ва это­го по­ло­же­ния по­ка нет.

КХД и адронные процессы

Ес­теств. об­ла­стью при­ме­не­ния тео­рии воз­му­ще­ний КХД по эф­фек­тив­но­му за­ря­ду яв­ля­ют­ся жё­ст­кие про­цес­сы с уча­сти­ем ад­ро­нов. Ос­но­ву та­ко­го при­ме­не­ния со­став­ля­ют кварк-ад­рон­ная ду­аль­ность и ре­нор­ма­ли­за­ци­он­ная ин­ва­ри­ант­ность ам­пли­туд и се­че­ний фи­зич. про­цес­сов. Ги­по­те­за кварк-ад­рон­ной ду­аль­но­сти ос­но­ва­на на том, что цвет­ные со­стоя­ния не на­блю­да­ют­ся, и со­сто­ит в том, что лю­бое бес­цвет­ное со­стоя­ние с дан­ны­ми кван­то­вы­ми чис­ла­ми мож­но пред­ста­вить ли­бо как су­пер­по­зи­цию ад­рон­ных со­стоя­ний, ли­бо как су­пер­по­зи­цию кварк-глю­он­ных со­стоя­ний с те­ми же со­хра­няю­щи­ми­ся кван­то­вы­ми чис­ла­ми. Эта ги­по­те­за при­сут­ст­ву­ет во всех при­ло­же­ни­ях КХД. Напр., пол­ное се­че­ние $\sigma$ ан­ни­ги­ля­ции элек­трон-по­зи­трон­ной па­ры в ад­ро­ны ($e^+e^- \to$ ад­ро­ны) за­ви­сит толь­ко от од­ной им­пульс­ной пе­ре­мен­ной – квад­ра­та 4-им­пуль­са па­ры $Q^2$ в сис­те­ме цент­ра масс. Ги­по­те­за кварк-ад­рон­ной ду­аль­но­сти по­зво­ля­ет при­рав­нять се­че­ние ан­ни­ги­ля­ции $\sigma$ к се­че­нию про­цес­са $e^+e^- \to$ квар­ки+глюо­ны. Обыч­но это се­че­ние за­пи­сы­ва­ют в ви­де $$\sigma(e^+e^- \to \text{адроны}=\sigma_0R(Q^2/\mu^2, \alpha_s(\mu^2)),\quad\tag{2}$$где $\sigma_0=4 \pi \alpha^2/3Q^2$ – се­че­ние ан­ни­ги­ля­ции па­ры $e^+e^-$ в па­ру $\mu^+ \mu^-$, рас­счи­ты­вае­мое по КЭД, $\alpha=e^2/4\pi \approx 1/137$ ($e$ – эле­мен­тар­ный элек­трич. за­ряд), $R$ – не­ко­то­рая без­раз­мер­ная функ­ция. Со­глас­но ре­нор­ма­ли­за­ци­он­ной ин­ва­ри­ант­но­сти, эта функ­ция, как и се­че­ние, не за­ви­сит от вы­бо­ра нор­ми­ров­ки $\mu^2$. По­ло­жив, что $\mu^2=Q^2$, по­лу­чим $$R(Q^2/\mu^2, \alpha_s(\mu^2))=R(1, \alpha_s(Q^2)),\quad\tag{3}$$где при дос­та­точ­но боль­ших $Q^2$ бла­го­да­ря свой­ст­ву асим­пто­тич. сво­бо­ды мож­но ис­поль­зо­вать тео­рию воз­му­ще­ний по $\alpha_s$. 

Вы­чис­ле­ния с учё­том как ан­ни­ги­ля­ции па­ры кварк-ан­тик­варк, так и из­лу­че­ния од­ним из до­пол­нит. глюо­нов (рис. 4) да­ют $$R=\sum e^2_q[1+\alpha_s(Q^2)/\pi+\dots],\quad\tag{4}$$где сум­ми­ро­ва­ние про­во­дит­ся по всем цве­там и аро­ма­там квар­ков, $e_q$ – за­ряд квар­ка в еди­ни­цах $e$, $\alpha_s(Q^2)$ оп­ре­де­ля­ет­ся фор­му­лой (1). Т. о., $R$ с рос­том $Q^2$ долж­но ло­га­риф­ми­че­ски при­бли­жать­ся к сум­ме квад­ра­тов за­ря­дов всех квар­ков всех цве­тов, то есть к т. н. пар­тон­но­му пре­де­лу.

Рис. 4. Диаграмма для сечения (вероятности) процесса е+е–→адроны с учётом как аннигиляции в пару кварк-антикварк, так и излучения одним из них дополнительного глюона.

В вы­ра­же­нии (4) от­бро­ше­ны не толь­ко по­прав­ки с бо­лее вы­со­ки­ми сте­пе­нями $\alpha_s$, но и сте­пен­ные по­прав­ки ти­па $(1/Q^2)^n$. Они воз­ни­ка­ют в тех слу­ча­ях, ко­гда боль­шой им­пульс $Q$ рас­пре­де­ля­ет­ся не по всем вир­ту­аль­ным ли­ни­ям фейн­ма­нов­ских диа­грамм рав­но­мер­но, а «об­хо­дит» к.-л. из них (напр., глю­он­ную ли­нию на рис. 4). 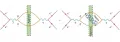Ма­лая ве­ли­чи­на квад­ра­та вир­ту­аль­но­го им­пуль­са со­от­вет­ст­вую­щей ли­нии не по­зво­ля­ет вос­поль­зо­вать­ся тео­ри­ей воз­му­ще­ний для вы­чис­ле­ния её вкла­да. Вы­ра­же­ния для та­ких диа­грамм ока­зы­ва­ют­ся про­пор­цио­наль­ны зна­че­ни­ям ва­ку­ум­ных сред­них квад­ра­тов глю­он­ных и квар­ко­вых по­лей. Эти зна­че­ния рас­смат­ри­ва­ют­ся как фе­но­ме­но­ло­гич. па­ра­мет­ры, т. е. под­би­ра­ют­ся в к.-л. од­ном экс­пе­ри­мен­те, а за­тем ис­поль­зу­ют­ся в дру­гих. [Они так­же мо­гут быть вы­чис­ле­ны ме­то­да­ми, не ис­поль­зую­щи­ми тео­рию воз­му­ще­ний, напр. ме­то­дом вы­чис­ле­ний на ре­шёт­ке (см. Ре­шё­точ­ные тео­рии по­ля).] Для ком­пен­са­ции раз­мер­но­стей, ко­то­ры­ми об­ла­да­ют эти па­ра­мет­ры, они вхо­дят в по­пра­воч­ные сла­гае­мые с мно­жи­те­ля­ми Q^–4 и Q^–6. Для учё­та наи­бо­лее су­ще­ст­вен­ной час­ти та­ких по­пра­вок в про­стей­шем слу­чае при­ме­ня­ют­ся пра­ви­ла сумм КХД, ко­то­рые ут­вер­жда­ют ра­вен­ст­во се­че­ний с учас­ти­ем ад­ро­на и се­че­ний с уча­сти­ем квар­ко­вых то­ков с те­ми же кван­то­вы­ми чис­ла­ми, ус­ред­нён­ных с не­ко­то­рым ве­сом по ин­тер­ва­лу, вклю­чаю­ще­му дан­ный ад­рон (по т. н. ин­тер­ва­лу ду­аль­но­сти). По по­ряд­ку ве­ли­чи­ны ин­тер­вал ду­аль­но­сти пред­став­ля­ет со­бой ха­рак­тер­ное рас­стоя­ние ме­ж­ду со­сед­ни­ми ре­зо­нан­са­ми (ре­зо­нанс­ны­ми час­ти­ца­ми) с оди­на­ко­вы­ми кван­то­вы­ми чис­ла­ми (спи­ном, чёт­но­стью, изо­то­пич. спи­ном и др.). Это да­ёт воз­мож­ность вы­ра­зить че­рез ва­ку­ум­ные сред­ние мас­сы и ши­рины низ­ко­ле­жа­щих ре­зо­нан­сов, напр. про­то­на или $\rho$-ме­зо­на.

Ха­рак­тер­ным свой­ст­вом се­че­ния ан­ни­ги­ля­ции, ко­то­рое по­зво­ли­ло не­по­сред­ст­вен­но ис­поль­зо­вать тео­рию воз­му­ще­ний, бы­ла за­ви­си­мость лишь от од­ной боль­шой им­пульс­ной пе­ре­мен­ной $Q^2$. В др. вы­со­ко­энер­ге­тич. про­цес­сах, кро­ме груп­пы боль­ших им­пульс­ных пе­ре­мен­ных $Q_1^2,\dots, Q_k^2 \gg m^2 \approx 1 $ ГэВ² ($m$ – мас­са ну­кло­на), име­ет­ся, как пра­ви­ло, и груп­па ма­лых пе­ре­мен­ных $p^2_1,\dots,p^2_r \approx m^2$ (напр., мас­сы на­чаль­ных и ко­неч­ных ре­ги­ст­ри­руе­мых ад­ро­нов), ко­то­рые, в от­ли­чие от слу­чая ан­ни­ги­ля­ции, не да­ют воз­мож­но­сти пе­ре­вес­ти всю за­ви­си­мость от боль­ших пе­ре­мен­ных $Q^2$ в эф­фек­тив­ный за­ряд $\alpha_s(Q^2)$.

Эту труд­ность уда­ёт­ся пре­одо­леть, напр., с по­мо­щью т. н. опе­ра­тор­но­го раз­ло­же­ния (или т. н. тео­ре­мы о фак­то­ри­за­ции), ко­то­рое до­ка­за­но в лю­бом по­ряд­ке тео­рии воз­му­ще­ний. Для се­че­ний жё­ст­ких про­цес­сов оно при­во­дит к мо­ди­фи­ци­ро­ван­ной пар­тон­ной мо­де­ли, в ко­то­рой на боль­ших рас­стоя­ни­ях рас­смат­ри­ва­ют­ся функ­ции рас­пре­де­ле­ния и фраг­мен­та­ции пар­то­нов, а на ма­лых – пар­тон­ные под­про­цес­сы. В этой мо­де­ли па­ра­метр $\mu^2$ од­но­вре­мен­но иг­ра­ет роль па­ра­мет­ра нор­ми­ров­ки и па­ра­мет­ра гра­ни­цы ме­ж­ду ма­лы­ми и боль­ши­ми им­пуль­са­ми (боль­ши­ми и ма­лы­ми рас­стоя­ния­ми).

Вслед­ст­вие за­ви­си­мо­сти се­че­ния под­про­цес­са толь­ко от боль­ших пе­ре­мен­ных $Q^2_i$ и $\mu^2$ (па­ра­метр $\mu^2$ так­же мо­жет быть вы­бран боль­шим, напр. $\mu^2=Q^2_1$) вы­чис­лить его мож­но с по­мо­щью тео­рии воз­му­ще­ний. Раз­ло­же­ние се­че­ния в ряд по $\alpha_s$ со­от­вет­ст­ву­ет учё­ту уп­ру­го­го рас­сея­ния на то­чеч­ном пар­то­не и по­сле­до­ва­тель­но­му учё­ту по­пра­вок за счёт не­то­чеч­но­сти квар­ка, ис­пус­ка­ния глюо­нов, а так­же ро­ж­де­ния кварк-ан­тик­вар­ко­вых пар. Од­на­ко се­че­ние про­цес­са не долж­но за­ви­сеть от вы­бо­ра па­ра­мет­ра $\mu^2$, по­это­му зна­ние за­ви­си­мо­сти се­че­ния под­про­цес­са от $\mu^2$ (из тео­рии воз­му­ще­ний) по­зво­ля­ет най­ти за­ви­си­мость от $\mu^2$ функ­ций рас­пре­де­ле­ния и фраг­мен­та­ции.

Экспериментальная проверка КХД

КХД пред­ска­зы­ва­ет спе­ци­фич. от­кло­не­ния от на­ив­ной пар­тон­ной мо­де­ли, свя­зан­ные с за­ви­си­мо­стью эф­фек­тив­но­го за­ря­да $\alpha_s$ и функ­ций рас­пре­де­ле­ния и фраг­мен­та­ции пар­то­нов от боль­шой им­пульс­ной пе­ре­мен­ной. Эти эф­фек­ты ка­че­ст­вен­но про­яв­ля­ют­ся во мно­гих экс­пе­ри­мен­таль­но на­блю­дае­мых жё­ст­ких про­цес­сах с уча­сти­ем ад­ро­нов. При этом все они ха­рак­те­ри­зу­ют­ся прак­ти­че­ски од­ной и той же ве­ли­чи­ной эф­фек­тив­но­го за­ря­да $\alpha_s$, при­ве­дён­но­го к мас­се Z-бо­зо­на. Пре­ж­де все­го это про­цес­сы глу­бо­ко не­уп­ру­го­го рас­сея­ния леп­то­нов на нук­ло­нах, где на­блю­да­ет­ся за­мет­ное от­кло­не­ние от скей­лин­га Бьёр­ке­на (см. Мас­штаб­ная ин­ва­ри­ант­ность), свя­зан­ное с за­ви­си­мо­стью функ­ций рас­пре­де­ле­ния от \mu^2=Q^2.

Бы­ли про­ве­де­ны рас­чё­ты ши­рин ад­рон­ных и леп­тон­ных рас­па­дов и рас­щеп­ле­ния уров­ней в квар­ко­ни­ях (напр., по вы­чис­ле­нию раз­но­сти масс $\Upsilon$- и $\eta_b$-ме­зо­нов, со­стоя­щих из тя­жё­лых $b$-квар­ка и $\tilde b$-ан­тик­вар­ка, а так­же $J/\psi$- и $\eta_c$-ме­зо­нов, состоящиx из $c$-квар­ка и $\tilde c$-ан­ти­квар­ка). Эти сис­те­мы иг­ра­ют для про­вер­ки КХД та­кую же роль, как атом водо­ро­да для кван­то­вой ме­ха­ни­ки в пе­ри­од её ста­нов­ле­ния. Для этих сис­тем на­блю­да­ет­ся не­пло­хое ко­ли­че­ст­вен­ное со­гла­сие тео­ре­тич. рас­чё­тов с экс­пе­ри­мен­том (осо­бен­но с учё­том глю­он­ных ра­ди­ац. по­пра­вок). Рас­пад тя­жё­лой $\Upsilon$-час­ти­цы в ад­ро­ны, со­глас­но КХД, идёт че­рез ан­ни­ги­ля­цию па­ры тя­жё­лых квар­ка и ан­тик­вар­ка $b \tilde b$ в три глюо­на, ко­то­рые пре­вра­ща­ют­ся за­тем в три ад­рон­ные струи. Та­кие ад­рон­ные струи с пред­ска­зан­ным уг­ло­вым рас­пре­де­ле­ни­ем дей­стви­тель­но на­блю­да­лись экс­пе­ри­мен­таль­но, что слу­жит экс­пе­рим. под­твер­жде­ни­ем век­тор­но­го ха­рак­те­ра глюо­нов.

Век­тор­ный ха­рак­тер глюо­на от­чёт­ли­во про­яв­ля­ет­ся и в уг­ло­вом рас­пре­де­ле­нии ад­рон­ных струй в про­цес­се ан­ни­ги­ля­ции па­ры $e^+e^-$ в три струи. Так­же на­блю­да­ет­ся ещё один ха­рак­тер­ный для КХД про­цесс – пря­мое глю­он-глю­он­ное взаи­мо­дей­ст­вие (рис. 2). Это ска­зы­ва­ет­ся, напр., в срав­ни­тель­но боль­шой ве­ли­чи­не от­но­ше­ния се­че­ний ро­ж­де­ния в про­тон-про­тон­ных столк­но­ве­ни­ях $K^-$- и $\pi^-$-ме­зо­нов с боль­ши­ми по­пе­реч­ны­ми им­пуль­са­ми (при от­сут­ст­вии глю­он-глю­он­но­го рас­сея­ния $K^-$-ме­зо­ны мог­ли бы ро­ж­дать­ся толь­ко за счёт т. н. мор­ских кварк-ан­тик­вар­ков $s$ и $\tilde u$, ко­ли­че­ст­во ко­то­рых в про­то­не не­зна­чи­тель­но).

Во 2-й пол. 1970-х гг. в КХД на­ча­ли раз­ви­вать­ся ме­то­ды вы­чис­ле­ния, не свя­зан­ные с раз­ло­же­ни­ем по кон­стан­те взаи­мо­дей­ст­вия. К ним от­но­сит­ся, напр., ме­тод ин­стан­то­нов, ос­но­ван­ный на раз­ло­же­нии урав­не­ний КХД в ма­лой ок­ре­ст­но­сти клас­сич. час­ти­це­по­доб­ных ре­ше­ний и пред­став­ляю­щий со­бой ана­лог ква­зи­клас­сич. при­бли­же­ния в кван­то­вой ме­ха­ни­ке. Осо­бен­но ши­ро­ко при­ме­ня­ют­ся в КХД чис­лен­ные ме­то­ды, ос­но­ван­ные на за­ме­не не­пре­рыв­но­го про­стран­ст­ва-вре­ме­ни на дис­крет­ную ре­шёт­ку, функ­цио­наль­ных ин­те­гра­лов (пред­став­ляю­щих со­бой на­блю­дае­мые фи­зич. ве­ли­чи­ны) – на мно­го­крат­ные ин­те­гра­лы, вы­чис­ляе­мые на ЭВМ с по­мо­щью ме­то­да Мон­те-Кар­ло. Это по­ка един­ст­вен­ный ре­гу­ляр­ный ме­тод, по­зво­ляю­щий вый­ти за рам­ки тео­рии воз­му­ще­ний. Най­ден­ные та­ким спо­со­бом па­ра­мет­ры мн. эле­мен­тар­ных час­тиц (мас­сы, кон­стан­ты рас­па­дов, маг­нит­ные мо­мен­ты) в пре­де­лах дос­тиг­ну­той точ­но­сти вы­чис­ле­ний ≈30% (ли­ми­ти­руе­мой мощ­но­стью совр. ЭВМ) со­гла­су­ют­ся с экс­пе­ри­мен­таль­ны­ми. Од­на­ко, по всей ве­ро­ят­но­сти, чис­лен­ным ме­то­дам в КХД при­над­ле­жит боль­шое бу­ду­щее.

КХД обес­пе­чи­ва­ет хо­ро­шее по­лу­ко­ли­че­ст­вен­ное (а в не­ко­то­рых слу­ча­ях и ко­ли­че­ст­вен­ное) объ­яс­не­ние ха­рак­тер­ных осо­бен­но­стей мн. вы­со­ко­энер­ге­тич. про­цес­сов с уча­сти­ем ад­ро­нов. Прин­ци­пи­аль­ное зна­че­ние для её даль­ней­шей про­вер­ки име­ют пре­ци­зи­он­ные экс­пе­ри­мен­ты при мак­си­маль­но вы­со­ких энер­ги­ях. Од­на­ко наи­бо­лее ост­рой ос­та­ёт­ся про­бле­ма удер­жа­ния цве­та в КХД. Ка­ким бу­дет ре­ше­ние этой про­бле­мы – ИК-удер­жа­ние, обу­слов­лен­ное рос­том эф­фек­тив­но­го за­ря­да при раз­де­ле­нии двух цвет­ных объ­ек­тов и ан­ти­эк­ра­ни­ров­кой цве­та за счёт ро­ж­де­ния из ва­куу­ма кварк-ан­тик­вар­ко­вых пар, пре­вра­щаю­щих даль­но­дей­ст­вую­щие си­лы ме­ж­ду квар­ка­ми (из-за об­ме­на без­мас­со­вы­ми глюо­на­ми) в ко­рот­ко­дей­ст­вую­щие ядер­ные си­лы меж­ду ад­ро­на­ми, или пе­ре­строй­ка ва­куу­ма из-за кон­ден­са­ции ИК глю­он­ных по­лей – по­ка не­яс­но. Но ка­ко­во бы оно ни бы­ло, КХД, как и тео­рия элек­тро­сла­бо­го взаи­мо­дей­ст­вия, пред­став­ля­ет со­бой сту­пень в на­прав­ле­нии соз­да­ния еди­ной тео­рии по­ля, объ­е­ди­няю­щей все вза­и­мо­дей­ст­вия эле­мен­тар­ных час­тиц (см. Ве­ли­кое объ­е­ди­не­ние, Су­пер­сим­мет­рия).