И́НДЕКСЫ КРИСТАЛЛОГРАФИ́ЧЕСКИЕ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
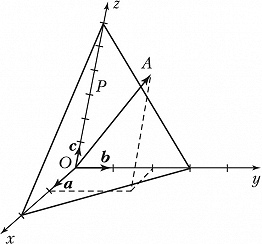
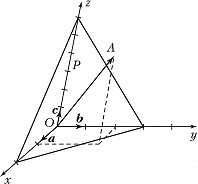
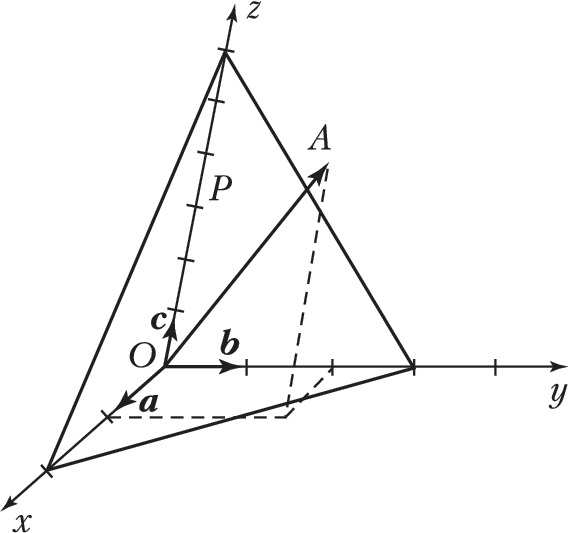
И́НДЕКСЫ КРИСТАЛЛОГРАФИ́ЧЕСКИЕ, три целых числа, определяющие расположение граней и атомных плоскостей кристалла в пространстве (индексы Миллера), а также направлений в кристалле и его рёбер (индексы Вейса) относительно кристаллографич. осей. Прямая и параллельное ей ребро, определяемые индексами Вейса $p_1,\, p_2,\, p_3$ (обозначаются $[p_1p_2p_3]$), проходят из начала координат $O$ в точку $A$, определяемую вектором $p_1{\bf a} + p_2{\bf b} + p_3{\bf c}$, где $a,\, b,\, c$ – периоды кристаллич. решётки (изображённая на рис. прямая $OA$ определяется индексами Вейса [124]).
Кристаллографич. плоскость отсекает на осях координат, построенных на векторах ${\bf a},\,{\bf b},\,{\bf c}$, отрезки $p'_1{\bf a},\, p'_2{\bf b},\, p'_3{\bf c}$ ($p'_1,\,p'_2,\,p'_3$ – целые числа). Целочисленные обратные отношения $1/p'_1:1/p'_2:1/p'_3=h:k:l$ определяют индексы Миллера ($hkl$) данной плоскости. Напр., для изображённой на рис. плоскости $P\, p'_1=2,\, p'_2= 3,\, p'_3 = 6$; величины, обратные этим, $1/2:1/3:1/6$ можно привести к целым числам $6/2:6/3:6/6= 3: 2: 1$, т. е. плоскость $P$ определяется индексами Миллера (321).
Равенство нулю одного или двух индексов Миллера означает, что плоскости параллельны одной или двум кристаллографич. осям. Отрицательные значения индексов Миллера соответствуют плоскостям, пересекающим оси координат в отрицательных направлениях. Совокупность симметричных граней одной простой формы кристалла обозначается $\{hkl\}$. При дифракции рентгеновских лучей индексы $h,\, k,\, l$ отражающей плоскости характеризуют одновременно положение дифракционного максимума в обратной решётке.