ЗВУ́КА АНА́ЛИЗ

Рис. 1. Периодический звуковой сигнал (а) и его спектр (б); ап – амплитуды спектральных составляющих.

ЗВУ́КА АНА́ЛИЗ, раз­ло­же­ние слож­но­го зву­ко­во­го сиг­на­ла на ряд про­стых со­став­ляю­щих. Ча­ще все­го при­ме­ня­ют­ся час­тот­ный и вре­мен­ной З. а. При час­тот­ном З. а. зву­ко­вой сиг­нал $p(t)$, где $t$ – вре­мя, $p$ – зву­ко­вое дав­ле­ние, пред­став­ля­ет­ся сум­мой его со­став­ляю­щих $p_i(t)$ в за­дан­ных по­ло­сах час­тот $Δf_i$. При вре­меннóм З. а. сиг­нал пред­став­ля­ет­ся сум­мой ко­рот­ких им­пуль­сов, ха­рак­те­ри­зую­щих­ся вре­ме­нем по­яв­ле­ния и ам­пли­ту­дой.

Рис. 2. Непериодический звуковой сигнал (а) и его спектр (б); a(f) – спектральная плотность сигнала.

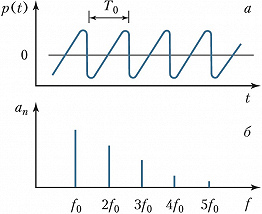
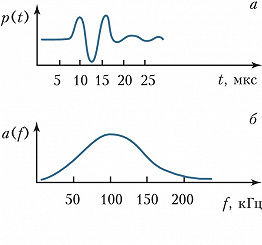
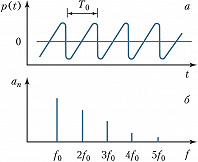
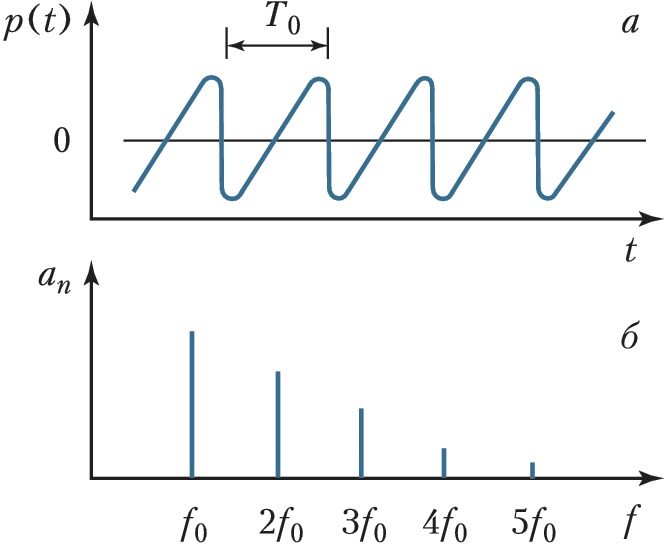
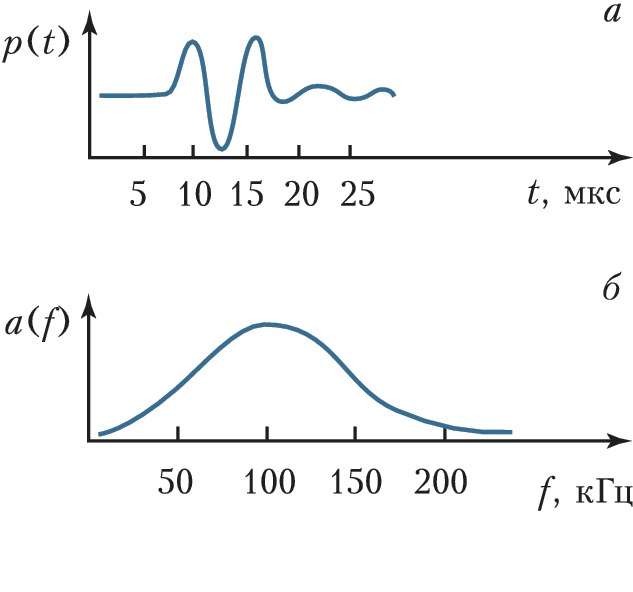
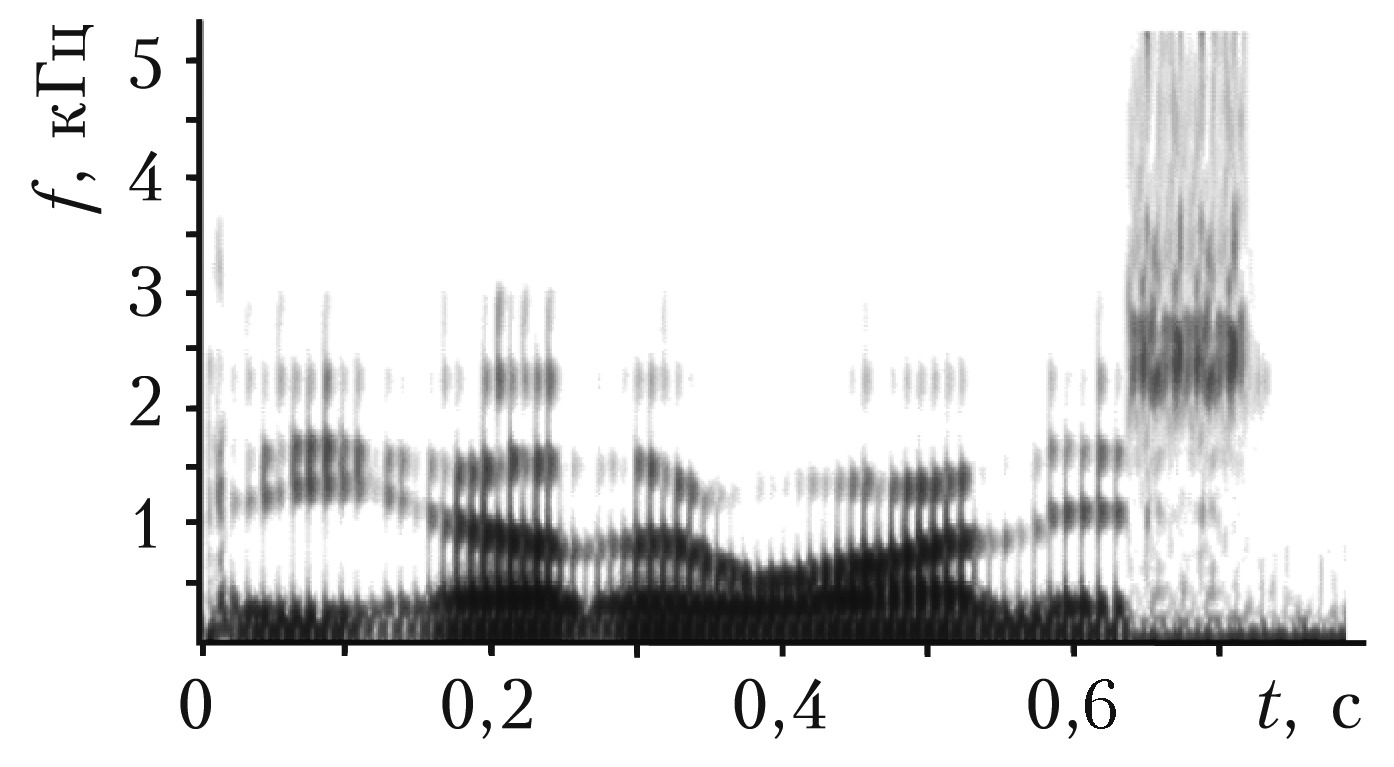
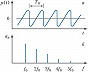
Ес­ли зву­ко­вой сиг­нал $p(t)$ пе­рио­ди­чен (рис. 1) (боль­шин­ст­во муз. зву­ков, глас­ные зву­ки ре­чи), то его пред­став­ля­ют в ви­де ря­да Фу­рье, в ко­то­ром час­то­ты $f$ об­ра­зу­ют гар­мо­нич. ряд $f_0,\: 2f_0, \: 3f_0$ и т. д., $f_0$ – низ­шая час­то­та ря­да, $T_0= 1/f_0$ – пе­ри­од зву­ко­во­го ко­ле­ба­ния. Ес­ли же зву­ко­вой сиг­нал $p(t)$ не­пе­ри­оди­чен, напр. од­но­крат­ный щел­чок (рис. 2), то его мож­но рас­смат­ри­вать как пе­рио­ди­че­ский с бес­ко­неч­но боль­шим пе­рио­дом $T_0$. При этом чис­ло гар­мо­ник ста­но­вит­ся бес­ко­неч­но боль­шим, а час­тот­ные ин­тер­ва­лы ме­ж­ду ни­ми – бес­ко­неч­но ма­лы­ми; та­кой сиг­нал пред­став­ля­ют в ви­де ин­те­гра­ла Фу­рье.

До по­яв­ле­ния элек­тро­аку­стич. ме­то­дов час­тот­ный З. а. про­во­ди­ли с по­мо­щью на­бо­ра ре­зо­на­то­ров аку­сти­че­ских с разл. соб­ст­вен­ны­ми час­то­та­ми, на­блю­дая, ка­кие из ре­зо­на­то­ров «от­кли­ка­ют­ся» на звук и с ка­кой гром­ко­стью. В на­стоя­щее вре­мя З. а. вы­пол­ня­ют по­сле пре­об­ра­зо­ва­ния зву­ко­во­го сиг­на­ла в элек­триче­ский с по­мо­щью элек­тро­аку­сти­че­ских пре­об­ра­зо­ва­те­лей – мик­ро­фо­на, гид­ро­фо­на и др. При­ме­ня­ют ли­бо па­рал­лель­ный, ли­бо по­сле­до­ва­тель­ный З. а. В пер­вом слу­чае элек­трич. сиг­нал про­пус­ка­ют че­рез на­бор по­лос­ных фильт­ров с ши­ри­ной по­ло­сы $Δf_𝑘 \:(𝑘$ – но­мер фильт­ра) и по­лу­ча­ют час­тот­ный спектр. Наи­бо­лее упот­ре­би­тель­ны ана­ли­за­то­ры с по­сто­ян­ной от­но­сит. ши­ри­ной по­ло­сы $Δf_𝑘 /(f_{ср})_{𝑘} [(f_{ср})_{𝑘}$  – ср. час­то­та фильт­ра], рав­ной 1, ¹/₃ или ¹/₆ ок­та­вы. Со­во­куп­ность на­пря­же­ний на вы­хо­де фильт­ров пред­став­ля­ет час­тот­ный спектр сиг­на­ла. В слу­чае не­ста­ционар­ных сиг­на­лов спектр ха­рак­те­ри­зу­ет­ся на­ко­п­лен­ны­ми за не­ко­то­рый ин­тер­вал вре­ме­ни сред­не­квад­ра­тич­ны­ми на­пря­же­ния­ми на вы­хо­де фильт­ров.

Бо­лее вы­со­кую раз­ре­шаю­щую спо­соб­ность обес­пе­чи­ва­ет ме­тод по­сле­до­ва­тель­но­го З. а. (ме­тод ге­те­ро­ди­ни­ро­ва­ния), при ко­то­ром с по­мо­щью спец. ге­не­ра­то­ра (ге­те­ро­ди­на) с ре­гу­ли­руе­мой час­то­той $f_г$ по­лу­ча­ют на­пря­же­ние с раз­но­ст­ной $f_г – f_с$ или сум­мар­ной $f_г + f_с$ час­то­той ($f_с$ – час­то­та сиг­на­ла). По­лос­ный фильтр с ши­ри­ной по­ло­сы $Δf$ на­стро­ен при этом на не­ко­то­рую фик­си­ро­ван­ную час­то­ту $f_п$. При плав­ном из­ме­не­нии $f_г$ все час­тот­ные со­став­ляю­щие сиг­на­ла по­сле­до­ва­тель­но об­ра­зу­ют с $f_г$ раз­но­ст­ную час­то­ту $f_г – f_с = f_п ± Δf/2$. За­ви­си­мость на­пря­же­ния на вы­хо­де фильт­ра от час­то­ты да­ёт ам­пли­туд­но-час­тот­ный спектр зву­ка. Ана­ли­за­то­ры ге­те­ро­дин­но­го ти­па про­во­дят З. а. с по­сто­ян­ной ши­ри­ной по­ло­сы.

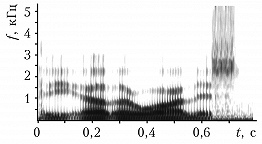
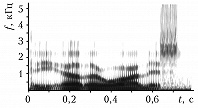
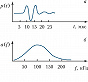
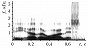
Час­тот­ные спек­тры мно­гих прак­ти­че­ски важ­ных зву­ков (речь, зву­ки го­ло­сов жи­вот­ных, шум ма­шин и ме­ха­низ­мов) из­ме­ня­ют­ся во вре­ме­ни. Что­бы про­сле­дить эти из­ме­не­ния, при­ме­ня­ют час­тот­но-вре­мен­ной, или со­но­гра­фи­че­ский, ана­лиз. Час­тот­ные спек­тры, по­лу­чен­ные за по­сле­до­ват. ин­тер­ва­лы вре­ме­ни, ото­бра­жа­ют­ся в ко­ор­ди­на­тах «час­то­та–вре­мя». Сте­пень по­чер­не­ния бу­ма­ги ха­рак­те­ри­зу­ет зна­че­ние спек­траль­ной со­став­ляю­щей на дан­ном ин­тер­ва­ле вре­ме­ни (рис. 3).

Рис. 3. Сонографическое изображение речевого сигнала.

Для З. а. на­ря­ду с ана­ло­го­вы­ми ме­тода­ми, ос­но­ван­ны­ми на при­ме­не­нии фильт­ров, ге­те­ро­дин­ных ана­ли­за­то­ров, со­но­гра­фов, ши­ро­ко при­ме­ня­ют­ся чис­лен­ные ме­то­ды с ис­поль­зо­ва­ни­ем ЭВМ. При­ме­не­ние ЭВМ по­зво­ля­ет вы­пол­нять как час­тот­ный, так и вре­мен­ной З. а. Воз­мож­но так­же раз­ло­же­ние зву­ко­во­го сиг­на­ла по от­лич­ным от си­ну­сои­даль­ных функ­ци­ям; так, боль­шую по­пу­ляр­ность при­об­рёл вейв­лет­ный ана­лиз зву­ка.

Для ана­ли­за слу­чай­ных зву­ко­вых сиг­на­лов при­ме­ня­ют кор­ре­ля­ци­он­ный ана­лиз, по­зво­ляю­щий оп­ре­де­лить сте­пень ста­ти­стич. взаи­мо­свя­зи ли­бо од­но­го и то­го же сиг­на­ла $p(t)$, но в разл. мо­мен­ты вре­ме­ни, от­стоя­щие на ин­тер­вал τ, ли­бо раз­ных зву­ко­вых сиг­на­лов $p_1(t)$ и $p_2(t)$, напр. зву­ко­во­го по­ля в раз­ных точ­ках про­стран­ст­ва. Ме­то­да­ми кор­ре­ля­ци­он­но­го ана­ли­за ре­ша­ют­ся та­кие за­да­чи, как пред­ска­за­ние ха­рак­те­ра из­ме­не­ния про­цес­са во вре­ме­ни, вы­де­ле­ние сла­бых аку­стич. сиг­на­лов на фо­не по­мех, из­ме­ре­ние ис­ка­же­ний ве­ща­тель­ных сиг­на­лов при их пе­ре­да­че элек­тро­аку­стич. сис­те­мой и др. По кор­ре­ля­ци­он­ным функ­ци­ям мо­гут быть най­де­ны мн. фи­зич. ха­рак­те­ри­сти­ки аку­стич. про­цес­сов, сис­тем и зву­ко­вых по­лей, пред­став­ляю­щие прак­тич. ин­те­рес.

З. а. при­ме­ня­ют при изу­че­нии свойств ис­точ­ни­ков зву­ка, сре­ды его рас­про­стра­не­ния, при об­на­ру­же­нии зву­ко­во­го сиг­на­ла на фо­не др. ме­шаю­щих зву­ков, при рас­по­зна­ва­нии зву­ко­во­го сиг­на­ла и т. п. Напр., ана­ли­зи­руя зву­ки жи­вот­ных, мож­но вы­яс­нить био­ло­гич. на­зна­че­ние этих зву­ков. На­блю­дая из­ме­не­ние спек­тров зву­ка с рас­стоя­ни­ем, вы­яв­ля­ют спо­соб­ность воз­душ­ной или вод­ной сре­ды про­во­дить, по­гло­щать и рас­сеи­вать звук. По спек­трам шу­мов серд­ца у лю­дей вы­пол­ня­ют аку­стич. ди­аг­но­сти­ку серд­ца. З. а. по­ле­зен при борь­бе с шу­мом и виб­ра­ция­ми на про­из-ве и транс­пор­те. Напр., зная спектр шу­ма ав­то­мо­биль­но­го дви­га­те­ля, мож­но рас­счи­тать ра­цио­наль­ную кон­ст­рук­цию глу­ши­те­ля. Зна­ние спек­тров ре­че­вых и муз. зву­ков не­об­хо­ди­мо для вы­бо­ра час­тот­ной ха­рак­те­ри­сти­ки элек­тро­аку­стич. пе­ре­даю­щих трак­тов, обес­пе­чи­ваю­щих тре­буе­мое ка­че­ст­во вос­про­из­ве­де­ния зву­ка. На ос­но­ве З. а. ра­бо­та­ют сис­те­мы ав­тома­тич. рас­по­зна­ва­ния ре­чи. Ме­то­ды вре­меннóго и час­тот­но­го З. а. ле­жат в ос­нове прин­ци­па дей­ст­вия гид­ро­ло­ка­то­ров и эхо­ло­тов.

З. а. в жи­вой при­ро­де про­из­во­дит­ся слу­хо­вы­ми ор­га­на­ми жи­вот­ных, при­чём, чем вы­ше на сту­пе­ни эво­лю­ци­он­ной ле­ст­ни­цы на­хо­дит­ся жи­вот­ное, тем слож­нее его З. а. Так, слух на­се­ко­мых ана­ли­зи­ру­ет звук толь­ко по его вре­меннóй струк­ту­ре, то­гда как ам­фи­бии и мле­копи­таю­щие (вклю­чая че­ло­ве­ка) име­ют раз­ви­тую сис­те­му З. а.: час­тот­но­го (па­рал­лель­но­го на улит­ке ор­га­на слу­ха) и час­тот­но-вре­мен­нó­го (в ней­рон­ных струк­ту­рах го­лов­но­го моз­га). Наи­бо­лее раз­ви­ты­ми фор­ма­ми З. а. об­ла­да­ют эхо­ло­ци­рую­щие жи­вот­ные – дель­фи­ны, ле­ту­чие мы­ши.