ВИНТОВО́Е ДВИЖЕ́НИЕ

Рис. 1.

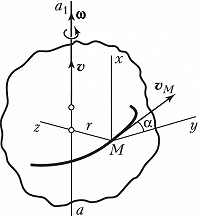
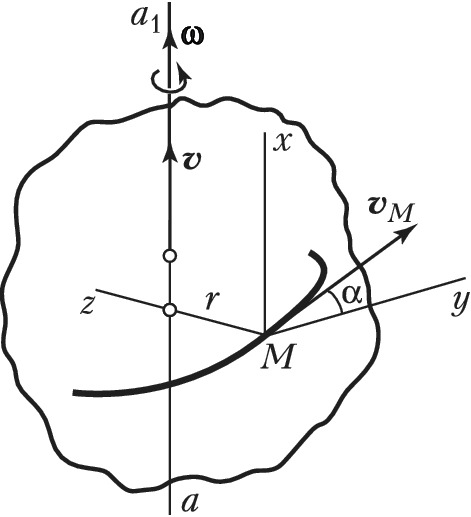
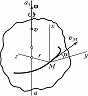
ВИНТОВО́Е ДВИЖЕ́НИЕ, дви­же­ние твёр­до­го те­ла, со­стоя­щее из пря­мо­ли­ней­но­го по­сту­па­тель­но­го дви­же­ния с не­ко­то­рой ско­ро­стью $𝒗$ и вра­ща­тель­но­го дви­же­ния с не­ко­то­рой уг­ло­вой ско­ро­стью $𝛚$ во­круг оси $aa_1$, па­рал­лель­ной на­прав­ле­нию ско­рос­ти по­сту­па­тель­но­го дви­же­ния (рис. 1). От­но­ше­ние $p=𝒗/𝛚$ , на­зы­вае­мое па­ра­мет­ром вин­то­во­го дви­же­ния, по­сто­ян­но, хо­тя са­ми ве­ли­чи­ны $𝒗$ и $𝛚$ мо­гут из­ме­нять­ся со вре­ме­нем.

Ось $aa_1$ на­зы­ва­ет­ся осью вин­то­во­го дви­же­ния; рас­стоя­ние $h$, про­хо­ди­мое лю­бой точ­кой те­ла, ле­жа­щей на оси $aa_1$, за вре­мя од­но­го обо­ро­та, на­зы­ва­ет­ся ша­гом вин­то­во­го дви­же­ния: $h=2πp$. Тра­ек­то­рии всех то­чек те­ла, не ле­жа­щих на оси $aa_1$, пред­став­ля­ют со­бой вин­то­вые ли­нии од­но­го и то­го же ша­га. Ско­рость $v_M$ лю­бой точ­ки $M$ те­ла, от­стоя­щей на рас­стоя­ние $r$ от оси $aa_1$, чис­лен­но рав­на $$v_M=\sqrt{v^2+r^2\omega ^2}.$$

Рис. 2.

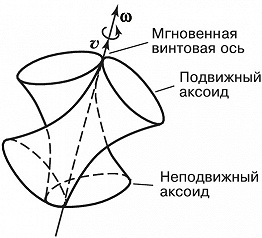
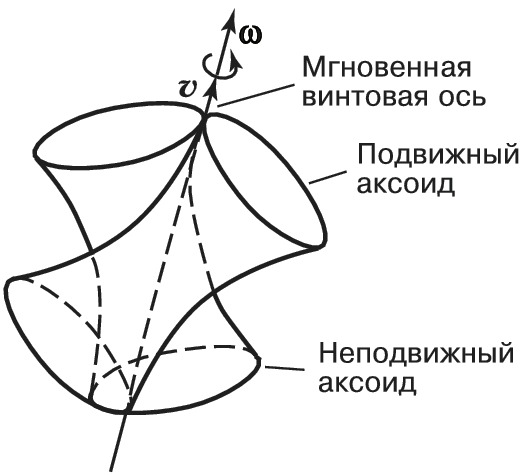
При про­из­воль­ном дви­же­нии твёр­до­го те­ла в ка­ж­дый мо­мент вре­ме­ни ско­ро­сти его то­чек ока­зы­ва­ют­ся та­ки­ми, как ес­ли бы те­ло со­вер­ша­ло вин­то­вое дви­же­ние. Это оз­на­ча­ет, что не­ко­то­рые точ­ки те­ла об­ра­зу­ют мгно­вен­ную вин­то­вую ось, их ско­ро­сти оди­на­ко­вы и на­прав­ле­ны вдоль этой оси. Ос­таль­ные точ­ки те­ла со­вер­ша­ют вра­щат. дви­же­ние во­круг мгно­вен­ной вин­то­вой оси. При этом мгно­вен­ная вин­то­вая ось не­пре­рыв­но из­ме­ня­ет своё по­ло­же­ние как по от­но­ше­нию к те­лу, так и по от­но­ше­нию к не­под­виж­ной сис­те­ме ко­ор­ди­нат, в ко­то­рой рас­смат­ри­ва­ет­ся дви­же­ние те­ла, об­ра­зуя две ли­ней­ча­тые по­верх­но­сти, со­при­ка­саю­щие­ся по пря­мой ли­нии, – под­виж­ный и не­под­виж­ный ак­сои­ды (рис. 2).