УМОЗАКЛЮЧЕ́НИЕ

УМОЗАКЛЮЧЕ́НИЕ, мыс­ли­тель­ная про­це­ду­ра не­по­средст­вен­но­го вы­ве­де­ния не­ко­то­ро­го вы­ска­зы­ва­ния, или су­ж­де­ния (на­зы­вае­мо­го за­клю­че­ни­ем), из од­но­го или не­сколь­ких др. вы­ска­зы­ва­ний (на­зы­вае­мых по­сыл­ка­ми). У. как по­зна­ват. при­ём, с по­мо­щью ко­то­ро­го осу­ще­ст­в­ля­ет­ся пре­об­ра­зо­ва­ние со­дер­жа­щей­ся в по­сыл­ках ин­фор­ма­ции, яв­ля­ет­ся про­стей­шей раз­но­вид­но­стью рас­су­ж­де­ния – про­цес­са обос­но­ва­ния вы­ска­зы­ва­ния по­сред­ст­вом по­ша­го­во­го вы­ве­де­ния его из др. вы­ска­зы­ва­ний; в У. пе­ре­ход от ар­гу­мен­тов (по­сы­лок) к обос­но­вы­вае­мо­му те­зи­су (за­клю­че­нию) про­ис­хо­дит в один шаг. В ло­ги­ке У. при­ня­то фор­му­ли­ро­вать сле­дую­щим об­ра­зом: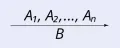$$\frac{A_1,A_2,...,A_n}{B},$$где над чер­той за­пи­сы­ва­ют­ся по­сыл­ки, под чер­той – за­клю­че­ние, а са­ма чер­та вы­ра­жа­ет акт вы­ве­де­ния за­клю­че­ния из по­сы­лок.

По сте­пе­ни обос­но­ван­но­сти вы­ве­де­ния (см. Вы­вод) за­клю­че­ния из по­сы­лок У. при­ня­то де­лить на де­мон­ст­ра­тив­ные и не­де­мон­ст­ра­тив­ные. В де­мон­ст­ра­тив­ных У. ис­тин­ность по­сы­лок обес­пе­чи­ва­ет по­лу­че­ние ис­тин­но­го за­клю­че­ния, ин­фор­ма­ция за­клю­че­ния со­став­ля­ет в них часть со­во­куп­ной ин­фор­ма­ции по­сы­лок. В не­де­мон­ст­ра­тив­ных У., на­про­тив, при пе­ре­хо­де от по­сы­лок к за­клю­че­нию име­ет ме­сто при­ра­ще­ние ин­фор­ма­ции, при этом ис­тин­ность по­сы­лок не га­ран­ти­ру­ет ис­тин­но­сти за­клю­че­ния.

Наи­бо­лее важ­ная и об­шир­ная раз­но­вид­ность де­мон­ст­ра­тив­ных У. – де­дук­тив­ные У. (см. Де­дук­ция, Сил­ло­гизм), ме­ж­ду по­сыл­ка­ми и за­клю­че­ни­ем ко­то­рых име­ет ме­сто от­но­ше­ние ло­гич. сле­до­ва­ния, т. е. са­ма ло­гич. фор­ма этих У. обес­пе­чи­ва­ет со­хра­не­ние ис­тин­но­сти при вы­ве­де­нии за­клю­че­ния из по­сы­лок. В де­мон­ст­ра­тив­ных У. др. ти­пов (напр., ма­те­ма­ти­че­ская ин­дук­ция, пол­ная ин­дук­ция, стро­гая ана­ло­гия) дос­то­вер­ность вы­во­да, по­лу­чае­мо­го из ис­тин­ных по­сы­лок, обу­слов­ле­на не толь­ко ло­гич. фор­мой вхо­дя­щих в У. вы­ска­зы­ва­ний, но и зна­че­ния­ми со­дер­жа­щих­ся в них де­ск­рип­тив­ных тер­ми­нов. Сре­ди не­де­мон­ст­ра­тив­ных У. наи­боль­ший ин­те­рес пред­став­ля­ют т. н. прав­до­по­доб­ные У., к ко­то­рым от­но­сят­ся, напр., об­рат­ная де­дук­ция, не­пол­ная ин­дук­ция, не­стро­гая ана­ло­гия, ста­ти­стич. вы­во­ды. Осн. сфе­рой при­ме­не­ния де­дук­тив­ных У. яв­ля­ют­ся точ­ные нау­ки (пре­ж­де все­го ма­те­ма­ти­ка и ло­ги­ка), в ко­то­рых предъ­яв­ля­ют­ся осо­бые тре­бо­ва­ния к стро­го­сти до­ка­за­тельств. Прав­до­по­доб­ные У. ис­поль­зу­ют­ся гл. обр. в эм­пи­рич. нау­ках для вы­дви­же­ния и ве­ри­фи­ка­ции ги­по­тез, по­лу­че­ния за­ко­но­по­доб­ных ут­вер­жде­ний, от­но­ся­щих­ся к ис­сле­дуе­мой пред­мет­ной об­лас­ти.