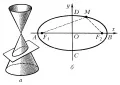
Э́ЛЛИПС

Э́ЛЛИПС (греч. ἔλλειψις – не­до­ста­ток, вы­па­де­ние, опу­ще­ние), ли­ния пе­ре­се­че­ния круг­ло­го ко­ну­са с плос­ко­стью, пе­ре­се­каю­щей од­ну его по­лость. Та­кое се­че­ние изо­бра­же­но на рис., а. Э. мо­жет быть так­же оп­ре­де­лён как гео­мет­рич. ме­сто то­чек $M$ плос­ко­сти $Oxy$ (рис., б), для ко­то­рых сум­ма рас­стоя­ний $r_1=F_1M$ и $r_2=F_2M$ до двух фик­си­ро­ван­ных то­чек $F_1$(–$c$,0) и $F_2$($c$,0) (фо­ку­сов Э.) этой плос­ко­сти есть ве­ли­чи­на по­сто­ян­ная: $r_1+r_2=2a$. Се­ре­ди­на $O$ от­рез­ка $F_1F_2$ (фо­кус­но­го рас­стоя­ния) на­зы­ва­ет­ся цен­тром эл­лип­са.

В пря­мо­уголь­ной сис­те­ме ко­ор­ди­нат $Oxy$ с на­ча­лом в цен­тре Э., на оси $Ox$ ко­то­рой ле­жат фо­ку­сы Э., урав­не­ние Э. при­ни­ма­ет т. н. ка­но­ни­че­ский вид$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\quad b^2=a^2-c^2$$где $a=OA=OB$ и $b=OC=OD$ – дли­ны боль­шой и ма­лой по­лу­осей Э. При $a=b$ фо­ку­сы $F_1$ и $F_2$ сов­па­да­ют и ука­зан­ное урав­не­ние оп­ре­де­ля­ет ок­руж­ность, ко­то­рая яв­ля­ет­ся ча­ст­ным слу­ча­ем эл­лип­са.

Э. – замк­ну­тая ли­ния вто­ро­го по­ряд­ка, она сим­мет­рич­на от­но­си­тель­но осей $Ox$ и $Oy$ и цен­тра Э. Фор­ма Э. (его вы­тя­ну­тость) оп­ре­де­ля­ет­ся экс­цен­три­си­те­том $e=c/a < 1$ (для ок­руж­но­сти $e=0$). Пря­мые, урав­не­ния ко­то­рых $x=-a/e$ и $x=a/e$, на­зы­ва­ют­ся ди­рек­три­са­ми Э.; от­но­ше­ние рас­стоя­ния точ­ки Э. до бли­жай­ше­го фо­ку­са к рас­стоя­нию до бли­жай­шей ди­рек­три­сы по­сто­ян­но и рав­но экс­цен­три­си­те­ту. Точ­ки $A$, $B$, $C$, $D$ пе­ре­се­че­ния Э. с ося­ми $Ox$, $Oy$ на­зы­ва­ют­ся вер­ши­на­ми Э. Пло­щадь, ог­ра­ни­чен­ная Э., рав­на πab.