Треугольник
Треуго́льник, многоугольник с тремя сторонами и тремя вершинами; фигура, образованная тремя точками, не лежащими на одной прямой, и тремя соединяющими их отрезками. Эти точки называют вершинами треугольника, а отрезки , соединяющие эти точки, – сторонами треугольника (рис. 1).
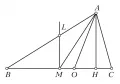 Рис. 1.
Рис. 1.
Длина любой стороны треугольника меньше суммы длин двух других его сторон. Сумма длин сторон треугольника называется его периметром. Иногда по каким-либо. соображениям выделяется одна из сторон, которая называется основанием треугольника; тогда две другие называются боковыми сторонами треугольника. В зависимости от соотношения длин сторон выделяются равносторонние (или правильные) треугольники (все стороны равны) и равнобедренные треугольники (две боковые стороны равны).
Три угла, каждый из которых образован двумя лучами, исходящими из вершины треугольника и проходящими через две другие вершины, называются внутренними углами треугольника. Сумма величин внутренних углов треугольника равна 180°. Различают треугольники остроугольные (все углы острые), тупоугольные (один угол тупой) и прямоугольные (один угол прямой). В прямоугольном треугольнике две стороны, прилегающие к прямому углу, называются катетами, а третья – гипотенузой.
Треугольник разбивает плоскость на две области – выпуклую – внутреннюю часть треугольника, и невыпуклую – внешнюю часть треугольника. Иногда при определении треугольника к нему относят и его внутреннюю часть.
Равными (конгруэнтными) называются треугольники, стороны и углы которых соответственно равны. В равных треугольниках против соответственно равных сторон лежат равные углы. Два треугольника равны, если три стороны одного треугольника соответственно равны трём сторонам другого треугольника; или если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника; или если сторона и прилегающие к ней углы одного треугольника соответственно равны стороне и прилегающим к ней углам другого треугольника.
Два треугольника называются подобными, если отношения длин соответствующих сторон равны и углы, заключённые между пропорциональными сторонами, также равны. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника (с одним и тем же коэффициентом пропорциональности); или если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны; или если два угла одного треугольника соответственно равны двум углам другого.
Отрезок перпендикуляра, опущенного из вершины треугольника на прямую, содержащую противоположную сторону, от вершины до этой прямой, называется высотой треугольника (длину этого перпендикуляра также называют высотой треугольника). Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Отрезок прямой, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Три медианы треугольника пересекаются в одной точке, называемой центроидом треугольника. Центроид делит медианы в отношении 2:1, считая от вершины. Отрезок биссектрисы внутреннего угла треугольника от вершины до противоположной стороны называется биссектрисой треугольника. Три биссектрисы внутренних углов треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник (см. ниже). Биссектриса внутреннего угла делит противоположную углу сторону на отрезки, пропорциональные другим сторонам. Прямая, перпендикулярная стороне треугольника и проходящая через её середину, называется серединным перпендикуляром треугольника. Три серединных перпендикуляра пересекаются в одной точке, являющейся центром описанной окружности (см. ниже). На рис. 1 показаны отрезки: – биссектриса угла при вершине , – медиана, – высота, – серединный перпендикуляр.
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией. Окружность, касающаяся всех трёх сторон треугольника, называется вписанной окружностью. На рис. 2 показана окружность , вписанная в треугольник , её радиус равен .
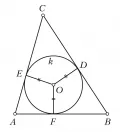 Рис. 2.
Рис. 2.
Окружность, проходящая через все вершины треугольника, называется описанной окружностью. На рис. 3 показана окружность , которая описана около треугольника , её радиус равен .
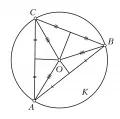 Рис. 3.
Рис. 3.
Некоторые основные связи между элементами треугольника состоят в следующем. Пусть – стороны треугольника (а также их длины), – противолежащие им углы. Для каждого треугольника справедливы теорема косинусов, теорема тангенсов и теорема синусов:
где – радиус описанной окружности.
Величина площади
где – высота, опущенная на сторону (или её продолжение), – полупериметр, – радиус вписанной окружности.
Радиус вписанной окружности
Решение треугольника состоит в нахождении неизвестных сторон и углов треугольника по его известным сторонам и углам.
