Сферическая тригонометрия
Сфери́ческая тригономе́трия, раздел геометрии, в котором изучаются связи между углами и сторонами сферических треугольников. Пусть – углы и – противолежащие им стороны (дуги большого круга) сферического треугольника (рис.).
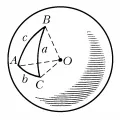 БРЭ. Т. 31.
БРЭ. Т. 31.
Они связаны основными формулами сферической тригонометрии
Здесь стороны измеряются соответствующими центральными углами, длины этих сторон равны соответственно , где – радиус сферы. Меняя обозначения углов (и сторон) по правилу круговой перестановки , можно получить другие формулы сферической тригонометрии, аналогичные указанным. Формулы сферической тригонометрии позволяют по любым трём элементам сферического треугольника определить три остальные (решить треугольник).
Для прямоугольных сферических треугольников (– гипотенуза, – катеты) формулы сферической тригонометрии существенно упрощаются, например:
Сферическая тригонометрия возникла значительно раньше плоской тригонометрии при решении задач астрономии. Свойства прямоугольных сферических треугольников, выражаемые формулами (1')–(3'), и различные случаи их решения были известны ещё Менелаю и Птолемею, арабский учёный Насирэддин ат-Туси (13 в.) рассмотрел все случаи решения косоугольных сферических треугольников, впервые указав решение в двух труднейших случаях. Л. Эйлер дал (1753, 1779) всю систему формул сферической тригонометрии.
