СФЕРИ́ЧЕСКАЯ ГЕОМЕ́ТРИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
СФЕРИ́ЧЕСКАЯ ГЕОМЕ́ТРИЯ, раздел геометрии, изучающий геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости.
Всякая плоскость, пересекающая сферу, даёт в сечении некоторую окружность; если секущая плоскость проходит через центр O сферы, то в сечении получается т. н. большой круг. Через каждые две точки A и B на сфере (рис., 1), кроме случая диаметрально противоположных точек, можно провести единственный большой круг. 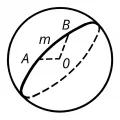Большие круги сферы являются её геодезическими линиями и потому в С. г. играют роль, аналогичную роли прямых в планиметрии. Однако в то время как отрезок прямой является кратчайшим путём между его концами, дуга большого круга на сфере будет кратчайшей лишь в случае, когда она короче дополнительной дуги. Во многих других отношениях С. г. также отлична от планиметрии; так, напр., в С. г. не существует параллельных геодезических: два больших круга всегда пересекаются, причём в двух точках.
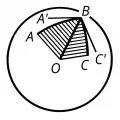Длину отрезка AB на сфере, т. е. дугу AmB (рис., 1) большого круга, измеряют соответствующим, пропорциональным ей, центральным углом AOB. Угол ABC (рис., 2), образованный на сфере дугами больших кругов, измеряют углом A'BC' между касательными к соответствующим дугам в точке пересечения B или двугранным углом, образованным плоскостями OBA и OBC.
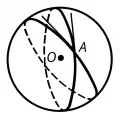При пересечении двух больших кругов на сфере образуются четыре сферич. двуугольника (рис., 3). Сферич. двуугольник определяется заданием своего угла. Площадь сферич. двуугольника определяется по формуле S=2R2A, где R – радиус сферы, A – угол двуугольника, выраженный в радианах.
Три больших круга, не пересекающихся в одной паре диаметрально противоположных точек, образуют на сфере восемь сферич. треугольников (рис., 4). 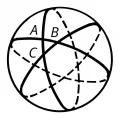Зная элементы (углы и стороны) одного из них, можно определить элементы всех остальных. Поэтому обычно рассматривают соотношения между элементами лишь одного треугольника, притом того, все стороны которого меньше половины большого круга (такие треугольники называются эйлеровыми). Стороны a, b, c сферич. треугольника измеряются плоскими углами трёхгранного угла OABC (рис., 5), углы A, B, C – двугранными углами того же трёхгранного угла. 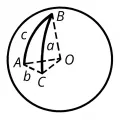Свойства сферич. треугольников во многом отличаются от свойств треугольников на плоскости (прямолинейных треугольников). Так, к известным трём случаям равенства прямолинейных треугольников для треугольников на сфере добавляется четвёртый: два треугольника равны, если равны их соответствующие углы (подобных треугольников на сфере не существует).
Равными треугольниками считаются те, которые могут быть совмещены после передвижения по сфере. Поэтому равные сферич. треугольники имеют равные элементы и одинаковую ориентацию. Треугольники, имеющие равные элементы и разл. ориентацию, называют симметричными, таковы, напр., треугольники АС'С и BCC' (рис., 6).
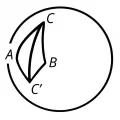Во всяком эйлеровом сферич. треугольнике каждая сторона меньше суммы и больше разности двух других; сумма всех сторон всегда меньше 2π. Сумма углов сферич. треугольника всегда меньше 3π и больше π. Разность s-π=ε, где s – сумма углов сферич. треугольника, называют сферич. избытком. Площадь сферич. треугольника есть S=R2ε, где R – радиус сферы. О соотношениях между углами и сторонами сферич. треугольника и об истории их изучения см. в ст. Сферическая тригонометрия.
