СТЕРЕОГРАФИ́ЧЕСКАЯ ПРОЕ́КЦИЯ

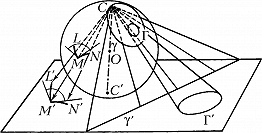
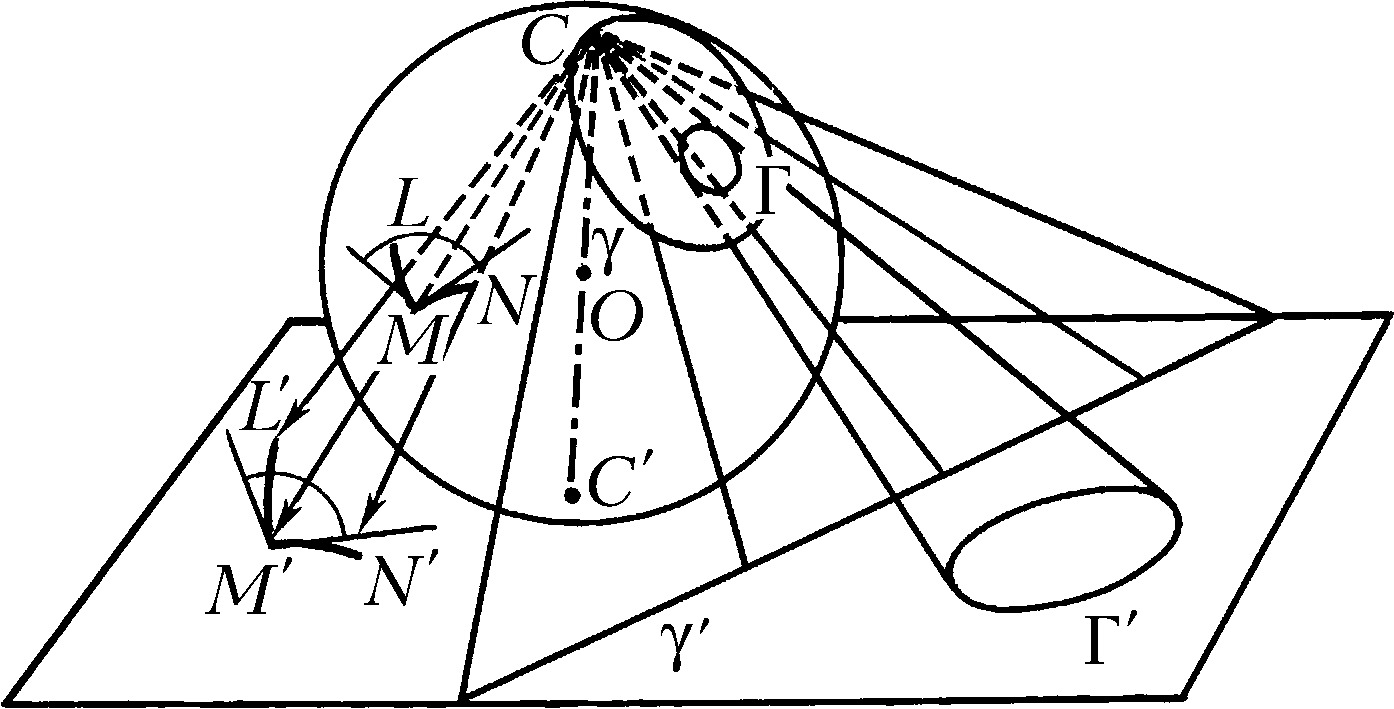
СТЕРЕОГРАФИ́ЧЕСКАЯ ПРОЕ́КЦИЯ (от сте­рео... и ...граф), со­от­вет­ст­вие ме­ж­ду точ­ка­ми сфе­ры и плос­ко­сти. Пусть за­да­ны сфе­ра с цен­тром O, C – не­ко­то­рая точ­ка сфе­ры (центр С. п.), и плос­кость, пер­пен­ди­ку­ляр­ная ра­диу­су OC и не про­хо­дя­щая че­рез точ­ку C (обыч­но эту плос­кость про­во­дят или че­рез центр сфе­ры, или че­рез точ­ку C´ – ко­нец диа­мет­ра CC´, про­хо­дя­ще­го че­рез центр сфе­ры). При С. п. ка­ж­дая точ­ка M сфе­ры, от­лич­ная от C, про­ек­ти­ру­ет­ся в точ­ку M´ плос­ко­сти, ко­то­рая яв­ля­ет­ся пе­ре­се­че­ни­ем плос­ко­сти и лу­ча CM (рис.). Со­от­вет­ст­вие ме­ж­ду точ­ка­ми на сфе­ре и точ­ка­ми на плос­ко­сти при С. п. бу­дет вза­им­но од­но­знач­ным, ес­ли ис­клю­чить из сфе­ры сам центр про­ек­ции C, ко­то­ро­му ни­ка­кая точ­ка сфе­ры не со­от­вет­ст­ву­ет, или до­пол­нить плос­кость во­об­ра­жае­мой точ­кой ∞ и счи­тать, что C и ∞ со­от­вет­ст­ву­ют друг дру­гу.

Осн. свой­ст­ва С. п.: 1) ок­руж­но­стям на сфе­ре со­от­вет­ст­ву­ют ок­руж­но­сти на плос­ко­сти (на рис. ок­руж­но­сти Γ на сфе­ре со­от­вет­ст­ву­ет ок­руж­ность Γ´ на плос­ко­сти, при­чём ок­руж­но­стям, про­хо­дя­щим че­рез центр С. п., со­от­вет­ст­ву­ют на плос­ко­сти пря­мые ли­нии (ок­руж­но­сти бес­ко­неч­но боль­шо­го ра­диу­са; на рис. γ и γ´); 2) со­от­вет­ст­вие, ус­та­нав­ли­вае­мое С. п., яв­ля­ет­ся кон­форм­ным, т. е. со­хра­ня­ет уг­лы (напр., угол LMN на сфе­ре ра­вен уг­лу L´M´N´ на плос­ко­сти).