РАЗРЫ́ВА ТО́ЧКА
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
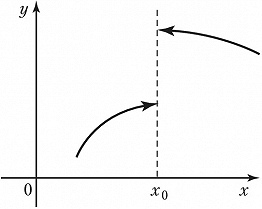
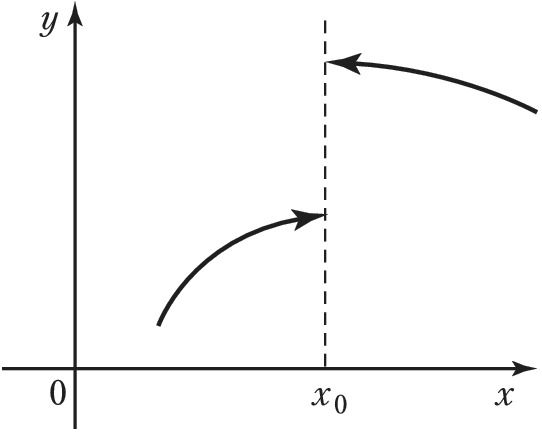
РАЗРЫ́ВА ТО́ЧКА, точка, в которой функция не является непрерывной. В простейшем случае в Р. т. $x_0$ (рис.) существуют односторонние пределы функции $f(x)$ справа и слева $$\lim_{h\gt 0,\,h→0}f(x_0+h)=f(x_0+0),\\ \lim_{h\lt 0,\,h→0}f(x_0+h)=f(x_0-0);$$ в этом случае $x_0$ называется Р. т. 1-го рода. Напр., Р. т. 1-го рода функции $[x]$ (целая часть $x$ – наибольшее целое число, меньшее или равное $x$) являются все целые числа. Разность $f(x_0+0)-f(x_0-0)$ называется скачком функции $f(x)$ в точке $x_0$. Если скачок равен нулю, то $x_0$ называется устранимой точкой разрыва. В этом случае существует $\lim_{x→x_0} f(x)$ и $x_0$ является Р. т. из-за того, что $f(x_0)$ не равна этому пределу или не определена в этой точке. Такой разрыв можно устранить положив $f(x_0)=\lim_{x→x_0} f(x)$; получится непрерывная в точке $x_0$ функция. Напр., точка $x_0=0$ является устранимой Р. т. функции $f(x)$, равной $1$ при $x≠0$ и $f(0)≠1$. Р. т. 1-го рода называется правильной, если $$f(x_0)=\frac{f(x_0-0)+f(x_0+0)}{2}$$Напр., точка $x_0=0$ является правильной Р. т. функции $\rm{sign}\,\it x$, равной $–1$ при $x\lt 0$, равной $0$ при $x=0$, и равной $1$ при $x\gt 0$.
Точка $x_0$ называется Р. т. 2-го рода функции $f(x)$, если эта функция определена в окрестности этой точки, за исключением, быть может, самой точки $x_0$, и хотя бы один из односторонних пределов не существует. Напр., для функций $\frac{1}{x}$, $\sin\frac{1}{x}$точка $x_0=0$ является Р. т. 2-го рода.
Функция, монотонная на интервале, может иметь на нём только Р. т. 1-го рода.