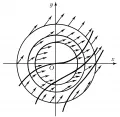
ПО́ЛЕ НАПРАВЛЕ́НИЙ

ПО́ЛЕ НАПРАВЛЕ́НИЙ, со­во­куп­ность то­чек плос­ко­сти $xOy$, в ка­ж­дой из ко­то­рых за­да­но оп­ре­де­лён­ное на­прав­ле­ние, изо­бра­жае­мое обыч­но стрел­кой, про­хо­дя­щей че­рез дан­ную точ­ку. Ес­ли да­но урав­не­ние $y′=f(x,y)$, то в ка­ж­дой точ­ке $(x_0,y_0)$ не­ко­то­рой об­лас­ти плос­ко­сти $xOy$ из­вест­но зна­че­ние уг­ло­во­го ко­эф. $k=f(x_0,y_0)$ ка­са­тель­ной к ин­те­граль­ной кри­вой, про­хо­дя­щей че­рез эту точ­ку; на­прав­ле­ние ка­са­тель­ной мож­но изо­бра­зить стрел­кой. Т. о., это диф­фе­рен­ци­аль­ное урав­не­ние оп­ре­де­ля­ет П. н., и на­обо­рот, П. н., за­дан­ное в не­ко­то­рой об­лас­ти плос­ко­сти $xOy$, оп­ре­де­ля­ет диф­фе­рен­ци­аль­ное урав­не­ние ви­да $y′=f(x,y)$. Про­во­дя дос­та­точ­но гус­тую сеть изо­клин (ли­ний оди­на­ко­во­го на­кло­на П. н. $f(x,y)=C$, где $C$ – по­сто­ян­ная), мож­но при­бли­жён­но по­стро­ить се­мей­ст­во ин­те­граль­ных кри­вых как со­во­куп­ность ли­ний, имею­щих в ка­ж­дой сво­ей точ­ке на­прав­ле­ние, сов­па­даю­щее с на­прав­ле­ни­ем по­ля. На рис. изо­бра­же­но П. н. урав­не­ния $y′=x^2+y^2$; тон­кие ли­нии (ок­руж­но­сти) – изо­кли­ны, жир­ные ли­нии – ин­те­граль­ные кри­вые.