ПЕРЕГИ́БА ТО́ЧКА

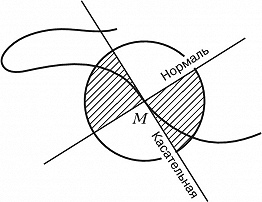
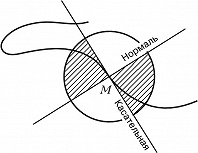
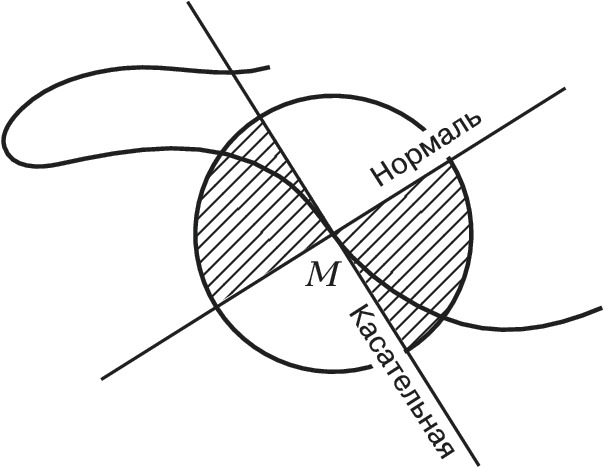
ПЕРЕГИ́БА ТО́ЧКА, точ­ка M пло­ской кри­вой, об­ла­даю­щая сле­дую­щи­ми свой­ст­ва­ми: в точ­ке M кри­вая име­ет един­ст­вен­ную ка­са­тель­ную; в дос­та­точ­но ма­лой ок­ре­ст­но­сти точ­ки M кри­вая рас­по­ло­же­на внут­ри од­ной па­ры вер­ти­каль­ных уг­лов, об­ра­зуе­мых ка­са­тель­ной и нор­ма­лью в точ­ке M. При­ме­ром П. т. яв­ля­ет­ся точ­ка (0, 0) кри­вой y=x³.

Пусть кри­вая за­да­на урав­не­ни­ем y=f(x), где функ­ция f(x) име­ет не­пре­рыв­ную 2-ю про­из­вод­ную f″(x). Ес­ли точ­ка (x₀, f(x₀)) яв­ля­ет­ся П. т., то f″(x₀)=0 (от­сю­да сле­ду­ет, что в П. т. кри­виз­на ли­нии рав­на ну­лю); об­рат­ное ут­вер­жде­ние не­вер­но. Напр., по­след­нее ра­вен­ст­во вы­пол­ня­ет­ся для кри­вой y=x⁴ в точ­ке (0, 0), хо­тя эта точ­ка не яв­ля­ет­ся П. т. Пол­ное ис­сле­до­ва­ние во­про­са о том, яв­ля­ет­ся ли дан­ная точ­ка кри­вой П. т., тре­бу­ет при­вле­че­ния про­из­вод­ных бо­лее вы­со­ких по­ряд­ков (ес­ли они су­ще­ст­ву­ют) или др. до­пол­нит. рас­смот­ре­ний.