ПАРАЛЛЕ́ЛЬНЫЕ ПРЯМЫ́Е
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ПАРАЛЛЕ́ЛЬНЫЕ ПРЯМЫ́Е, прямые, которые лежат в одной плоскости и не пересекаются. В евклидовой геометрии через точку, не лежащую на данной прямой, проходит только одна такая прямая. Это утверждение равносильно V постулату Евклида (о параллельных). См. Пятый постулат.
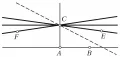
В Лобачевского геометрии в плоскости через точку $C$ (рис.) вне данной прямой $AB$ проходит бесконечное множество прямых, не пересекающих $AB$. Из них параллельными к $AB$ называются только две. Прямая $CE$ называется параллельной к прямой $AB$ в направлении от $A$ к $B$, если: 1) точки $B$ и $E$ лежат по одну сторону от прямой $AC$; 2) прямая $CE$ не пересекает прямую $AB$; всякий луч, проходящий внутри угла $ACE$, пересекает луч $AB$. Аналогично определяется прямая $CF$, параллельная к $AB$ в направлении от $B$ к $A$.
