ПАПИ́РУСЫ МАТЕМАТИ́ЧЕСКИЕ

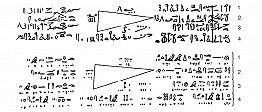
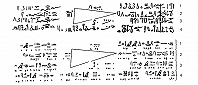
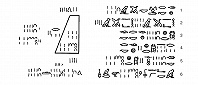
ПАПИ́РУСЫ МАТЕМАТИ́ЧЕСКИЕ, па­мят­ни­ки ма­те­ма­ти­че­ской нау­ки Древ­не­го Егип­та, от­но­ся­щие­ся к пе­рио­ду Сред­не­го цар­ст­ва (ок. 21 – ок. 18 вв. до н. э.). Наи­бо­лее из­вест­ны па­пи­рус Рин­да, хра­ня­щий­ся час­тич­но в Лон­до­не (в Бри­тан­ском му­зее) и час­тич­но в Нью-Йор­ке, и Мо­с­ков­ский па­пи­рус, хра­ня­щий­ся в Му­зее изо­бра­зит. ис­кусств им. А. С. Пуш­ки­на.

Фрагмент папируса Ринда, написанного иератическим письмом, и его перевод на иерографическую запись. Вычисление плошади треугольника.

Па­пи­рус Рин­да на­зван по име­ни его вла­дель­ца, егип­то­ло­га А. Г. Рин­да, впер­вые изу­чен и из­дан на нем. язы­ке в 1877; его на­зы­ва­ют так­же па­пи­ру­сом Ах­ме­са – по име­ни его со­ста­ви­те­ля – пис­ца Ах­ме­са (ок. 2000 до н. э.). Па­пи­рус Рин­да пред­став­ля­ет со­бой ре­ше­ние 84 за­дач, имею­щих при­клад­ной ха­рак­тер; эти за­да­чи от­но­сят­ся к дей­ст­ви­ям с дро­бя­ми, оп­ре­де­ле­нию пло­ща­ди пря­мо­уголь­ни­ка, тре­уголь­ни­ка, тра­пе­ции и кру­га (по­след­няя при­ни­ма­ет­ся рав­ной пло­ща­ди квад­ра­та со сто­ро­ной ⁸/₉ диа­мет­ра), объ­ё­ма пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да и ци­лин­д­ра; име­ют­ся так­же ариф­ме­тич. за­да­чи на про­пор­цио­наль­ное де­ле­ние, оп­ре­де­ле­ние со­от­но­ше­ний ме­ж­ду ко­ли­че­ст­вом зер­на и по­лу­чаю­ще­го­ся из не­го хле­ба или пи­ва; ре­ше­ние од­ной за­да­чи (79-й) сво­дит­ся к вы­чис­ле­нию сум­мы гео­мет­рич. про­грес­сии. Од­на­ко для ре­ше­ния этих за­дач не да­ёт­ся ни­ка­ких об­щих пра­вил, не го­во­ря уже о по­пыт­ках ка­ких-ни­будь тео­ре­тич. обоб­ще­ний.

Фрагмент Московского папируса, написанного иератическим письмом, и его перевод на иерографическую запись. Вычисление объёма усечённой пирамиды.

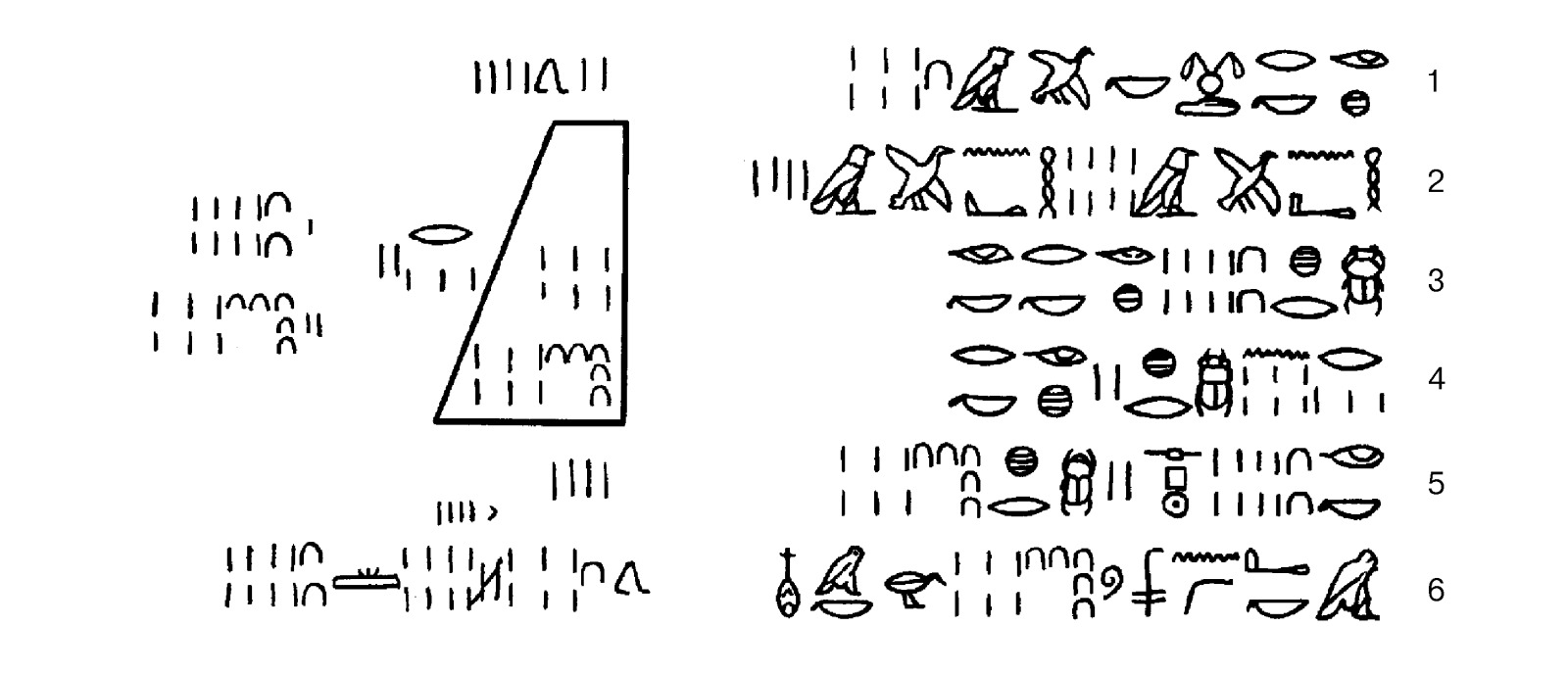
Мо­с­ков­ский па­пи­рус изу­чал­ся егип­то­ло­га­ми Б. А. Ту­рае­вым (1917) и В. В. Стру­ве (1927); пол­но­стью из­дан на нем. язы­ке в 1930. В нём со­б­ра­ны ре­ше­ния 25 за­дач при­мер­но та­ко­го же ти­па, как и в па­пи­ру­се Рин­да; осо­бый ин­те­рес пред­став­ля­ют 14-я и 10-я за­да­чи. Ре­ше­ние пер­вой из них ос­но­ва­но на точ­ной фор­му­ле объ­ё­ма усе­чён­ной пи­ра­ми­ды с квад­рат­ным ос­но­ва­ни­ем. В 10-й за­да­че вы­чис­ля­ет­ся бо­ко­вая по­верх­ность по­лу­ци­лин­д­ра, вы­со­та ко­то­ро­го рав­на диа­мет­ру, что яв­ля­ет­ся пер­вым в ма­те­ма­тич. лит-ре при­ме­ром оп­ре­де­ле­ния пло­ща­ди кри­вой по­верх­но­сти.