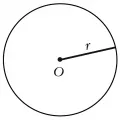
ОКРУ́ЖНОСТЬ

Рис. 1.

ОКРУ́ЖНОСТЬ, замк­ну­тая пло­ская кри­вая, все точ­ки ко­то­рой на­хо­дят­ся на од­ном и том же рас­стоя­нии от дан­ной точ­ки (цен­тра О.), ле­жа­щей в той же плос­ко­сти, что и кри­вая. От­ре­зок $r$, со­еди­няю­щий центр О. с к.-л. её точ­кой (а так­же дли­на это­го от­рез­ка), на­зы­ва­ет­ся ра­диу­сом О. (рис. 1).

Рис. 2.

От­ре­зок, со­еди­няю­щий две точ­ки О., на­зы­ва­ет­ся хор­дой (рис. 2). Хор­да, про­хо­дя­щая че­рез центр О., на­зы­ва­ет­ся диа­мет­ром. Диа­метр яв­ля­ет­ся наи­боль­шей из хорд. Диа­метр, ко­то­рый про­хо­дит че­рез се­ре­ди­ну хор­ды, пер­пен­ди­ку­ля­рен к ней.

Рис. 3.

Рис. 4.

Впи­сан­ным уг­лом на­зы­ва­ет­ся угол, об­ра­зо­ван­ный дву­мя хор­да­ми, имею­щи­ми об­щий ко­нец (рис. 3). Цен­траль­ным уг­лом на­зы­ва­ет­ся угол, об­ра­зо­ван­ный дву­мя ра­диу­са­ми. Впи­сан­ный угол из­ме­ря­ет­ся по­ло­ви­ной ду­ги, на ко­то­рую он опи­ра­ет­ся, и ра­вен по­ло­ви­не цен­траль­но­го уг­ла, за­клю­чаю­ще­го ту же ду­гу. Угол, об­ра­зо­ван­ный дву­мя се­ку­щи­ми, из­ме­ря­ет­ся по­лу­раз­но­стью дуг, за­клю­чён­ных ме­ж­ду его сто­ро­на­ми (рис. 4).

Рис. 5.

Че­рез точ­ку на О. мож­но про­вес­ти од­ну ка­са­тель­ную, при­чём она пер­пен­ди­ку­ляр­на ра­диу­су, со­еди­няю­ще­му эту точ­ку и центр О. (рис. 5). Ес­ли из точ­ки $M$ вне О. про­ве­де­ны се­ку­щая и ка­са­тель­ная к О., то про­из­ве­де­ние рас­стоя­ний от точ­ки $M$ до то­чек пе­ре­се­че­ния с О. рав­но квад­ра­ту дли­ны ка­са­тель­ной от точ­ки $M$ до О. (рис. 6).

Рис. 6.

От­но­ше­ние дли­ны О. к её диа­мет­ру од­но и то же для всех О.; это от­но­ше­ние есть транс­цен­дент­ное чис­ло, обо­зна­чае­мое греч. бу­к­вой $\pi=$ 3,14159... (см. Чис­ло $\pi$). Дли­на О. $l$ и её ра­ди­ус $r$ свя­за­ны ра­вен­ст­вом $l=2 \pi r$. Часть плос­ко­сти, ог­ра­ни­чен­ная О. и со­дер­жа­щая её центр, на­зы­ва­ет­ся кру­гом. С точ­ки зре­ния ана­ли­тич. гео­мет­рии О. яв­ля­ет­ся цен­траль­ной ли­ни­ей вто­ро­го по­ряд­ка, урав­не­ние ко­то­рой в пря­мо­уголь­ной сис­те­ме ко­ор­ди­нат име­ет вид $$(x-a)^2 +(y-b)^2=r^2,$$где $a$, $b$ – ко­ор­ди­на­ты цен­тра ок­руж­ности. О. – част­ный слу­чай эл­лип­са.