Осо́бая то́чка дифференциа́льного уравне́ния, точка, в которой одновременно обращаются в нуль и числитель, и знаменатель правой части дифференциального уравнения

$$\dfrac{dy}{dx} = \dfrac{P(x,y)}{Q(x,y)}, \tag{*}$$где $P$ и $Q$ – непрерывно дифференцируемые функции. Предполагая особую точку расположенной в начале координат и используя формулу Тейлора, уравнение $(*)$ можно представить в виде

$\dfrac{dy}{dx}=\dfrac{\gamma x+\delta y +P_1(x,y)}{\alpha x +\beta y+ Q_1(x,y)},$где $P_1(x,y)$ и $Q_1(x,y)$ – бесконечно малые по отношению к $\sqrt{x^2+y^2}$. Характер поведения интегральных кривых около особой точки зависит от корней $\lambda_1$ и $\lambda_2$ характеристического уравнения

$\begin{vmatrix} \alpha-\lambda & \beta\\ \gamma & \delta-\lambda\\ \end{vmatrix} = 0.$Точнее, если $\lambda_1 \neq \lambda_2$ и $\lambda_1\lambda_2 \gt 0$ или $\lambda_1=\lambda_2$, то особая точка есть узел; все интегральные кривые, проходящие через точки достаточно малой окрестности узла, входят в него. Если $\lambda_1 \neq \lambda_2$ и $\lambda_1\lambda_2 \lt 0$, то особая точка есть седло; в окрестности седла четыре интегральные кривые (сепаратрисы) входят в особую точку, а между ними располагаются интегральные кривые типа гиперболы. Если $\lambda_{1,2}=-a \pm ib$, $a \neq 0$, $b \neq 0$, то особая точка есть фокус; все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса. Если, наконец, $\lambda_{1,2}=\pm ib$, $b \neq 0$, то характер особой точки не определяется одними линейными членами в разложениях $P(x,y)$ и $Q(x,y)$, как это имело место во всех перечисленных случаях; здесь особая точка может быть фокусом или центром, а может иметь и более сложный характер. В окрестности центра все интегральные кривые являются замкнутыми и содержат центр внутри себя.

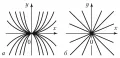Рис. 1. Особая точка дифференциального уравнения.Рис. 1. Особая точка дифференциального уравнения.

Так, например, начало координат является узлом для уравнений $y'=2y/x$ ($\lambda_1=1$, $\lambda_2=2$; рис. 1, а) и $y'=y/x$ ($\lambda_1=\lambda_2=1$; рис. 1, б), седлом для уравнения $y'=-y/x$ ($\lambda_1=-1$, $\lambda_2=1$; рис. 2), фокусом для уравнения $y'=(x+y)/(x-y)$ ($\lambda_1=1-i$, $\lambda_2=1+i$; рис. 3) и центром для уравнения $y'=-x/y$ ($\lambda_1=-i$, $\lambda_2=i$; рис. 4).

Если $\Delta= \begin{vmatrix} \alpha & \beta\\ \gamma & \delta\\ \end{vmatrix}= 0$, то особая точка называется особой точкой высшего порядка. Особые точки высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае когда функции $P(x,y)$ и $Q(x,y)$ аналитические, окрестность особой точки высшего порядка может распадаться на области: $D_1$ – заполненные интегральными кривыми, обоими концами входящими в особую точку (эллиптические области), $D_2$ – заполненные интегральными кривыми, одним концом входящими в особую точку (параболические области), и $D_3$ – области, ограниченные двумя интегральными кривыми, входящими в особую точку, между которыми расположены интегральные кривые типа гипербол (гиперболические области) (рис. 5). Рис. 2, 3, 4, 5, 6. Особая точка дифференциального уравнения.Рис. 2, 3, 4, 5, 6. Особая точка дифференциального уравнения.Если нет интегральных кривых, входящих в особую точку, то особая точка называется точкой устойчивого типа. Окрестность устойчивой особой точки состоит из замкнутых интегральных кривых, содержащих особую точку внутри себя, между которыми расположены спирали (рис. 6).

Изучение особых точек дифференциальных уравнений, т. е. по существу изучение поведения семейств интегральных кривых в окрестности особой точки, составляет один из разделов качественной теории дифференциальных уравнений и играет важную роль в приложениях, в частности в вопросах устойчивости движения.