Обратная функция
Обра́тная фу́нкция, функция , которая получается из данной функции , если из соотношения выразить через . Более подробно это означает следующее. Пусть функция определена на множестве , и пусть – множество её значений. Обратной по отношению к называется такая функция , которая определена на множестве и каждому ставит в соответствие такое , что . Таким образом, для нахождения функции , обратной к функции , необходимо решить уравнение относительно . Например, обратной функцией к является ; обратной функцией к является .
Отображение, задаваемое функцией , обратной к , является (левым) обратным к отображению, задаваемому функцией . При этом имеет место тождество для всех из множества .
Для функции обратная функция может быть многозначной. Например, обратной функцией к является , ; обратной функцией к является , (см. Обратные тригонометрические функции). Для однозначности обратной функции необходимо и достаточно, чтобы данная функция принимала различные значения при различных значениях аргумента, т. е. чтобы при . Для однозначности обратной функции к функции достаточно, чтобы была строго монотонной функцией. Это условие является и необходимым, если функция определена и непрерывна на числовом промежутке; в этом случае обратная функция также определена, строго монотонна и непрерывна на числовом промежутке. При этом, если функция имеет производную и , то обратная функция также имеет производную и .
В случае, когда обратная функция к функции многозначна, рассматривается такой числовой промежуток, на котором строго монотонна, тогда для на этом промежутке обратная функция однозначна. Например, для функции , обратная функция есть ; для , , обратная функция есть ; для функции , , обратная функция есть .
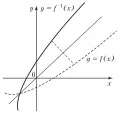
Иногда обратная функция к функции обозначается . Если обратная функция однозначна, то при всех из области определения функции и при всех из области определения функции . Графики (рис.) функций и симметричны относительно биссектрисы первого и третьего координатных углов.