ВЫ́ПУКЛОЕ МНО́ЖЕСТВО

ВЫ́ПУКЛОЕ МНО́ЖЕСТВО, мно­же­ст­во то­чек в евк­ли­до­вом или дру­гом век­тор­ном про­стран­ст­ве, ко­то­рое вме­сте с лю­бы­ми дву­мя точ­ка­ми со­дер­жит весь со­еди­няю­щий их от­ре­зок. Пе­ре­се­че­ние лю­бой со­во­куп­но­сти В. м. есть В. м. За­мы­ка­ние В. м. (т. е. ре­зуль­тат при­сое­ди­не­ния к В. м. всех его пре­дель­ных то­чек) да­ёт вы­пук­лое мно­же­ст­во.

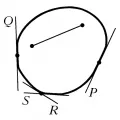
Че­рез ка­ж­дую точ­ку гра­ни­цы В. м. (см. Гра­ни­ца мно­же­ст­ва) на плос­ко­сти про­хо­дит хо­тя бы од­на опор­ная пря­мая, имею­щая с ней об­щую точ­ку, но не рас­се­каю­щая это мно­же­ст­во (на рис. P, Q, R, S – опор­ные пря­мые).

В трёх­мер­ном про­стран­ст­ве че­рез ка­ж­дую точ­ку гра­ни­цы В. м. про­хо­дит хо­тя бы од­на опор­ная плос­кость, де­ля­щая про­стран­ст­во на два по­лу­про­стран­ст­ва и та­кая, что это В. м. ле­жит в од­ном из замк­ну­тых по­лу­про­странств, по­ро­ж­дён­ных этой плос­ко­стью.

Замк­ну­тое В. м. есть пе­ре­се­че­ние ко­неч­но­го или бес­ко­неч­но­го чис­ла замк­ну­тых по­лу­про­странств. Пе­ре­се­че­ние ко­неч­но­го чис­ла замк­ну­тых по­лу­про­странств есть вы­пук­лый мно­го­гран­ник.