ПЕРИОДИ́ЧЕСКАЯ ФУ́НКЦИЯ

ПЕРИОДИ́ЧЕСКАЯ ФУ́НКЦИЯ, функ­ция, зна­че­ния ко­то­рой не из­ме­ня­ют­ся при до­бав­ле­нии к зна­че­ни­ям её ар­гу­мен­та не­ко­то­ро­го не рав­но­го ну­лю чис­ла T, на­зы­вае­мо­го пе­рио­дом функ­ции. Напр., sinx и cosx – П. ф. с пе­рио­дом 2π; tgx и ctgx – П. ф. с пе­рио­дом π; {x} – дроб­ная часть чис­ла x – П. ф. с пе­рио­дом 1.

Функ­ция f(x), оп­ре­де­лён­ная на мно­же­ст­ве E, яв­ля­ет­ся П. ф., ес­ли су­ще­ст­ву­ет чис­ло T≠0 та­кое, что для лю­бо­го x∈E зна­че­ния x+T и x-T так­же при­над­ле­жат E и f(x±T)=f(x). Ес­ли П. ф. f(x) не­пре­рыв­на на ка­ком-ни­будь ин­тер­ва­ле и f(x) не рав­на то­ж­де­ст­вен­но по­сто­ян­ной на этом ин­тер­ва­ле, то для неё су­ще­ст­ву­ет наи­мень­ший по­ло­жи­тель­ный пе­ри­од T и лю­бой пе­ри­од этой функ­ции име­ет вид kT, k=±1,±2,... .

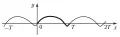
Для по­строе­ния гра­фи­ка П. ф. с пе­рио­дом T>0 дос­та­точ­но по­стро­ить её гра­фик на от­рез­ке [0,T], то­гда весь гра­фик по­лу­ча­ет­ся сдви­гом по­стро­ен­ной час­ти на ±T,±2T,... (рис.).

Сум­ма, раз­ность, про­из­ве­де­ние и ча­ст­ное П. ф. с оди­на­ко­вым пе­рио­дом яв­ля­ют­ся П. ф. с тем же пе­рио­дом. Про­из­вод­ная П. ф. так­же П. ф. с тем же пе­рио­дом. Пер­во­об­раз­ная П. ф. яв­ля­ет­ся П. ф. толь­ко то­гда, ко­гда ин­те­грал от этой функ­ции по от­рез­ку с дли­ной, рав­ной пе­рио­ду, ра­вен ну­лю; при этом пер­во­об­раз­ная П. ф. яв­ля­ет­ся П. ф. с тем же пе­рио­дом.

Сум­ма П. ф. с раз­ны­ми пе­рио­да­ми яв­ля­ет­ся П. ф. толь­ко то­гда, ко­гда их пе­рио­ды со­из­ме­ри­мы. Напр., sin2x+cos3x – П. ф. с пе­рио­дом 2π; sinx+sinpx не яв­ля­ет­ся П. ф.; это – при­мер поч­ти пе­рио­ди­че­ской функ­ции.

П. ф. ком­плекс­но­го пе­ре­мен­но­го мо­жет иметь ком­плекс­ный пе­ри­од. Напр., e^z – П. ф. с пе­рио­дом 2πi, e^(1+i)z – П. ф. с пе­рио­дом π(1+i). Не­пре­рыв­ная П. ф. мо­жет иметь два ком­плекс­ных пе­рио­да T₁ и T₂, от­но­ше­ние ко­то­рых не рав­но дей­ст­ви­тель­но­му чис­лу. Ес­ли T₁, T₂ – наи­мень­шие по мо­ду­лю пе­рио­ды, то лю­бой пе­ри­од име­ет вид k₁T₁+k₂T₂, k₁=0,±1,±2,..., k₂=0,±1,±2,... . Та­кие функ­ции на­зы­ва­ют­ся двоя­ко­пе­рио­ди­че­ски­ми; их при­ме­ры да­ют эл­лип­ти­че­ские функ­ции.