МАТЕМАТИ́ЧЕСКАЯ СТАТИ́СТИКА

МАТЕМАТИ́ЧЕСКАЯ СТАТИ́СТИКА, раз­дел ма­те­ма­ти­ки, по­свя­щён­ный ма­те­ма­тич. ме­то­дам сис­те­ма­ти­за­ции, об­ра­бот­ки и ис­поль­зо­ва­ния ста­ти­стич. дан­ных для на­уч. и прак­тич. вы­во­дов.

Предмет и метод математической статистики

Под ста­ти­стич. дан­ны­ми обыч­но по­ни­ма­ют чи­сло­вую ин­фор­ма­цию, из­вле­кае­мую из ре­зуль­та­тов вы­бо­роч­ных об­сле­до­ва­ний, ре­зуль­та­ты се­рии не­точ­ных из­ме­ре­ний и во­об­ще лю­бую сис­те­му ко­ли­че­ст­вен­ных дан­ных.

Ме­тод ис­сле­до­ва­ния, опи­раю­щий­ся на рас­смот­ре­ние ста­ти­стич. дан­ных о тех или иных со­во­куп­но­стях объ­ек­тов, на­зы­ва­ет­ся ста­ти­сти­че­ским. Ста­ти­стич. ме­тод ис­поль­зу­ет­ся во мн. об­лас­тях зна­ния. Од­на­ко чер­ты ста­ти­стич. ме­то­да в при­ме­не­нии к объ­ек­там разл. при­ро­ды столь раз­но­об­раз­ны, что бы­ло бы бес­смыс­лен­но объ­е­ди­нять, напр., со­ци­аль­но-эко­но­мич. ста­ти­сти­ку, звёзд­ную ста­ти­сти­ку и т. п. в од­ну нау­ку.

Об­щие чер­ты ста­ти­стич. ме­то­да в разл. об­лас­тях зна­ния сво­дят­ся к под­счё­ту чис­ла объ­ек­тов, вхо­дя­щих в те или иные груп­пы, рас­смот­ре­нию рас­пре­де­ле­ния ко­ли­че­ст­вен­ных при­зна­ков, при­ме­не­нию вы­бо­роч­но­го ме­то­да (в слу­ча­ях, ко­гда де­таль­ное ис­сле­до­ва­ние всех объ­ек­тов об­шир­ной со­во­куп­но­сти за­труд­ни­тель­но), ис­поль­зо­ва­нию ве­ро­ят­но­стей тео­рии при оцен­ке дос­та­точ­но­сти чис­ла на­блю­де­ний для тех или иных вы­во­дов и при оцен­ке точ­но­сти по­лу­чае­мых ре­зуль­та­тов. Эта фор­маль­ная ма­те­ма­тич. сто­ро­на ста­ти­стич. ме­то­дов ис­сле­до­ва­ния, не свя­зан­ная со спе­ци­фи­кой при­ро­ды изу­чае­мых объ­ек­тов, и со­став­ля­ет пред­мет ма­те­ма­тич. ста­ти­сти­ки.

Связь математической статистики с теорией вероятностей

Связь М. с. с тео­ри­ей ве­ро­ят­но­стей име­ет в раз­ных слу­ча­ях разл. ха­рак­тер. Тео­рия ве­ро­ят­но­стей изу­ча­ет не лю­бые яв­ле­ния, а яв­ле­ния слу­чай­ные и имен­но «ве­ро­ят­но­ст­но слу­чай­ные», т. е. та­кие, для ко­то­рых име­ет смысл го­во­рить о со­от­вет­ст­вую­щих им рас­пре­де­ле­ни­ях ве­ро­ят­но­стей. Тем не ме­нее тео­рия ве­ро­ят­но­стей иг­ра­ет оп­ре­де­лён­ную роль и при ста­ти­стич. изу­че­нии мас­со­вых яв­ле­ний лю­бой при­ро­ды, ко­то­рые мо­гут не от­но­сить­ся к ка­те­го­рии ве­ро­ят­но­ст­но слу­чай­ных. Это осу­ще­ст­в­ля­ет­ся че­рез ос­но­ван­ные на тео­рии ве­ро­ят­но­стей тео­рию вы­бо­роч­но­го ме­то­да и тео­рию оши­бок из­ме­ре­ний (см. Оши­бок тео­рия). В этих слу­ча­ях ве­ро­ят­но­ст­ным за­ко­но­мер­но­стям под­чи­не­ны не са­ми изу­чае­мые яв­ле­ния, а приё­мы их ис­сле­до­ва­ния.

При ста­ти­стич. ис­сле­до­ва­нии ве­ро­ят­но­ст­ных яв­ле­ний в пол­ной ме­ре на­хо­дят при­ме­не­ние та­кие ос­но­ван­ные на тео­рии ве­ро­ят­но­стей раз­де­лы М. с., как тео­рия про­вер­ки ста­ти­стич. ги­по­тез, тео­рия ста­ти­стич. оцен­ки рас­пре­де­ле­ний ве­ро­ят­но­стей или па­ра­мет­ров этих рас­пре­де­ле­ний. При ис­поль­зо­ва­нии этих раз­де­лов М. с. тре­бу­ет­ся, что­бы са­ми изу­чае­мые яв­ле­ния под­чи­ня­лись дос­та­точ­но оп­ре­де­лён­ным ве­ро­ят­но­ст­ным за­ко­но­мер­но­стям. Напр., ста­ти­стич. изу­че­ние ре­жи­ма тур­бу­лент­ных вод­ных по­то­ков или флук­туа­ций в ра­дио­при­ём­ных уст­рой­ст­вах про­из­во­дит­ся на ос­но­ве тео­рии ста­цио­нар­ных слу­чай­ных про­цес­сов. Од­на­ко при­ме­не­ние той же тео­рии к ана­ли­зу слу­чай­ных про­цес­сов в эко­но­ми­ке мо­жет при­вес­ти к гру­бым ошиб­кам вви­ду то­го, что вхо­дя­щее в оп­ре­де­ле­ние ста­цио­нар­но­го про­цес­са пред­по­ло­же­ние о на­ли­чии со­хра­няю­щих­ся в те­че­ние дли­тель­но­го вре­ме­ни не­из­мен­ных рас­пре­де­ле­ний ве­ро­ят­но­стей в этом слу­чае, как пра­ви­ло, не­при­ем­ле­мо.

Ве­ро­ят­но­ст­ные за­ко­но­мер­но­сти про­яв­ля­ют­ся в ста­ти­стич. дан­ных в си­лу боль­ших чи­сел за­ко­на (напр., час­то­ты со­бы­тий близ­ки к их ве­ро­ят­но­стям, а сред­ние зна­че­ния – к ма­те­ма­тич. ожи­да­ни­ям).

Простейшие приёмы статистического описания

Изу­чае­мая со­во­куп­ность из $n$ объ­ек­тов мо­жет по к.-л. при­зна­ку $A$ раз­би­вать­ся на клас­сы $A_1, A_2, ..., A_r$. Со­ответ­ст­вую­щее это­му раз­бие­нию ста­ти­стич. рас­пре­де­ле­ние за­да­ёт­ся при по­мо­щи ука­за­ния чис­лен­но­стей $n_1, n_2, ..., n_r$ отд. клас­сов, где $\sum_{i=1}^{r} n_i = n$. Вме­сто чис­лен­но­стей час­то ука­зы­ва­ют со­от­вет­ст­вую­щие от­но­сит. час­то­ты $h_i=n_i/n, i=1, 2, ..., r$, удов­ле­тво­ряю­щие со­от­но­ше­нию $\sum_{i=1}^{r} h_i = 1$.

Ес­ли изу­че­нию под­ле­жит не­ко­то­рый ко­ли­че­ст­вен­ный при­знак, то его ста­ти­стич. рас­пре­де­ле­ние в со­во­куп­но­сти из $n$ объ­ек­тов мож­но за­дать, пе­ре­чис­лив не­по­сред­ст­вен­но на­блю­дён­ные зна­че­ния при­зна­ка $x_1, x_2, ..., x_n$. Од­на­ко при боль­ших $n$ та­кой спо­соб гро­моз­док и в то же вре­мя не вы­яв­ля­ет су­ще­ст­вен­ных свойств рас­пре­де­ле­ния. При боль­ших $n$ на прак­ти­ке обыч­но не пе­ре­чис­ля­ют на­блю­дён­ные зна­че­ния при­зна­ка $x_1,x_2,...,x_n$, а ис­хо­дят лишь из чис­лен­но­стей клас­сов, по­лу­чаю­щих­ся при груп­пи­ров­ке на­блю­дён­ных зна­че­ний по над­ле­жа­ще вы­бран­ным ин­тер­ва­лам.

Рис. 1.

Рис. 2.

Рис. 3.

Обыч­но груп­пи­ров­ка по 10–20 ин­тер­ва­лам, в ка­ж­дый из ко­то­рых по­па­да­ет не бо­лее 15–20% на­блю­дён­ных зна­че­ний при­зна­ка, ока­зы­ва­ет­ся дос­та­точ­ной для до­воль­но пол­но­го вы­яв­ле­ния всех су­ще­ст­вен­ных свойств 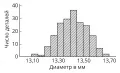рас­пре­де­ле­ния и на­дёж­но­го вы­чис­ле­ния по груп­по­вым чис­лен­но­стям осн. ха­рак­те­ри­стик рас­пре­де­ле­ния. По та­ким груп­пи­ро­ван­ным дан­ным со­став­ля­ет­ся гис­то­грам­ма, даю­щая пред­став­ле­ние о рас­пре­де­ле­нии при­зна­ка. Гис­то­грам­ма, со­став­лен­ная на ос­но­ве груп­пи­ров­ки с ма­лы­ми ин­тер­ва­ла­ми, обы­ч­но име­ет не­ре­гу­ляр­ный вид и не от­ража­ет су­ще­ст­вен­ных свойств рас­пре­де­ле­ния. С др. сто­ро­ны, груп­пи­ров­ка по слиш­ком круп­ным ин­тер­ва­лам мо­жет при­вес­ти к по­те­ре яс­но­го пред­став­ле­ния о ха­рак­те­ре рас­пре­де­ле­ния и к гру­бым ошиб­кам при вы­чис­ле­нии сред­не­го и др. ха­рак­те­ри­стик 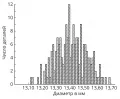рас­пре­де­ле­ния. В ка­че­ст­ве при­ме­ра на рис. 1 при­ве­де­на гис­то­грам­ма рас­пре­де­ле­ния диа­мет­ра не­ко­то­рой де­та­ли (изу­ча­лась вы­бор­ка из 200 де­та­лей) при дли­не ин­тер­ва­ла груп­пи­ров­ки 0,05 мм, на рис. 2 – гис­то­грам­ма то­го же рас­пре­де­ле­ния при ин­тер­ва­ле груп­пи­ров­ки 0,01 мм и на рис. 3 – гис­то­грам­ма при ин­тер­ва­ле груп­пи­ров­ки 0,20 мм.

Про­стей­ши­ми свод­ны­ми ха­рак­те­ри­сти­ка­ми рас­пре­де­ле­ния од­но­го ко­ли­че­ст­вен­но­го при­зна­ка яв­ля­ют­ся вы­бо­роч­ное сред­нее$$\overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_i$$

и вы­бо­роч­ное сред­нее квад­ра­тич­ное откло­не­ние $D=S/\sqrt{n}$ или вы­бо­роч­ная дис­пер­сия $D^2=S^2/n$, где $$S^2=\sum_{i=1}^{n} (x_i-\overline{x})^2.$$

При вы­чис­ле­нии $\overline{x}$, $S^2$ и $D$ по груп­пи­ро­ван­ным дан­ным поль­зу­ют­ся фор­му­ла­ми $$\overline{x}=\frac{1}{n}\sum_{k=1}^{r}n_ka_k=\sum_{k=1}^{r}h_ka_k,$$

$$S^2=\sum_{k=1}^{r}n_k(a_k-\overline{x})^2 = \sum_{k=1}^{r}n_ka_k^2-n\overline{x}^2$$

или $$D^2=\sum_{i=1}^{r}h_ka_k^2-\overline{x}^2 $$

где $r$ – чис­ло ин­тер­ва­лов груп­пи­ров­ки, $a_k$ – их се­ре­ди­ны. Ес­ли ма­те­ри­ал сгруп­пи­ро­ван по слиш­ком круп­ным ин­тер­ва­лам, то та­кой под­счёт да­ёт гру­бые ре­зуль­та­ты и ино­гда в та­ких слу­ча­ях вво­дят спец. по­прав­ки на груп­пи­ров­ку.

Связь статистических распределений с вероятностными. Оценка параметров. Проверка статистических гипотез

Вы­ше бы­ли из­ло­же­ны не­ко­то­рые про­стей­шие приё­мы ста­ти­стич. опи­са­ния, ко­то­рое яв­ля­ет­ся до­воль­но об­шир­ной дис­ци­п­ли­ной с хо­ро­шо раз­ра­бо­тан­ной сис­те­мой по­ня­тий и тех­ни­кой вы­чис­ле­ний. При­ё­мы ста­ти­стич. опи­са­ния ин­те­рес­ны, од­на­ко не са­ми по се­бе, а как сред­ст­во для по­лу­че­ния из ста­ти­стич. ма­те­риа­ла вы­во­дов о за­ко­но­мер­но­стях, ко­то­рым под­чи­ня­ют­ся изу­чае­мые яв­ле­ния, и о при­чи­нах, при­во­дя­щих в ка­ж­дом отд. слу­чае к тем или иным ста­ти­стич. рас­пре­де­ле­ни­ям.

Напр., дан­ные, по ко­то­рым по­лу­че­ны гис­то­грам­мы на рис. 1, 2, 3, бы­ли со­б­ра­ны с це­лью ус­та­нов­ле­ния точ­но­сти из­го­тов­ле­ния де­та­лей, рас­чёт­ный диа­метр ко­то­рых ра­вен 13,40 мм, при нор­маль­ном хо­де про­из­вод­ст­ва. Про­стей­шим до­пу­ще­ни­ем, ко­то­рое мо­жет быть в этом слу­чае обос­но­ва­но не­ко­то­ры­ми тео­ре­тич. со­об­ра­же­ния­ми, свя­зан­ны­ми с цен­траль­ной пре­дель­ной тео­ре­мой, яв­ля­ет­ся пред­по­ло­же­ние, что диа­мет­ры отд. де­та­лей мож­но рас­смат­ри­вать как реа­ли­за­ции слу­чай­ной ве­ли­чи­ны $X$, имею­щей нор­маль­ное рас­пре­де­ле­ние ве­ро­ят­но­стей

$$ \mathbf{P} \{ X < x \}=\frac{1}{\sqrt{2\pi\sigma }}\int_{-\infty }^{x}e^{-(t-a)^2/(2\sigma )^2}dt.\tag{*}$$

Ес­ли это до­пу­ще­ние вер­но, то па­ра­мет­ры $a$ и $σ^2$ – сред­нее и дис­пер­сию ве­ро­ят­но­ст­но­го рас­пре­де­ле­ния мож­но с дос­та­точ­ной точ­но­стью оце­нить по со­от­вет­ствую­щим ха­рак­те­ри­сти­кам ста­ти­стич. рас­пре­де­ле­ния (т. к. чис­ло на­блю­де­ний $n$ = 200 в этом слу­чае дос­та­точ­но ве­ли­ко), взяв в ка­че­ст­ве $a$ ве­ли­чи­ну $\overline{x}$ и в ка­че­ст­ве $σ^2$ – ве­ли­чи­ну $D^2$. Од­на­ко в ка­че­ст­ве оцен­ки для тео­ре­тич. дис­пер­сии $σ^2$ пред­по­чи­та­ют не ста­ти­стич. дис­пер­сию $D^2=S^2/n$, а не­сме­щён­ную оцен­ку

$$s^2=S^2/(n-1).$$

Даль­ней­шие све­де­ния об оцен­ке па­ра­мет­ров тео­ре­тич. рас­пре­де­ле­ний ве­ро­ят­но­стей см. в статьях Ста­ти­сти­че­ская оцен­ка, До­ве­ри­тель­ный ин­тер­вал.

Уже упо­ми­на­лось, что пред­по­ло­же­ние о том, что ре­зуль­та­ты на­блю­де­ний мож­но рас­смат­ри­вать как реа­ли­за­ции слу­чай­ной ве­ли­чи­ны $X$, под­чи­нён­ной то­му или ино­му рас­пре­де­ле­нию, напр. нор­маль­но­му рас­пре­де­ле­нию ( * ), ино­гда мож­но обос­но­вать тео­ре­тич. со­об­ра­же­ния­ми. Од­на­ко на прак­ти­ке час­то воз­ни­ка­ет за­да­ча о про­вер­ке ги­по­те­зы о том, что слу­чай­ная ве­ли­чи­на $X$ име­ет за­дан­ное рас­пре­де­ле­ние. Под­роб­нее об этом см. в ст. Ста­ти­сти­че­ских ги­по­тез про­вер­ка.

Все ос­но­ван­ные на тео­рии ве­ро­ят­но­стей пра­ви­ла ста­ти­стич. оцен­ки па­ра­мет­ров и про­вер­ки ги­по­тез дей­ст­ву­ют лишь с оп­ре­де­лён­ным зна­чи­мо­сти уров­нем $ω<1$, т. е. мо­гут при­во­дить к оши­боч­ным ре­зуль­та­там с ве­ро­ят­но­стью $α=1-ω$. Напр., ес­ли пред­по­ло­жить, что слу­чай­ная ве­ли­чи­на $X$ име­ет нор­маль­ное рас­пре­де­ле­ние с из­вест­ной тео­ре­тич. дис­пер­си­ей $σ^2$, и про­во­дить оцен­ку $a$ по $\overline{x}$ по пра­ви­лу $$\overline{x}-\frac{k\sigma }{\sqrt{n}} < a < \overline{x} + \frac{k\sigma }{\sqrt{n}},$$

то ве­ро­ят­ность ошиб­ки, т. е. ве­ро­ят­ность то­го, что ука­зан­ное не­ра­вен­ст­во не вы­пол­не­но, бу­дет рав­на чис­лу $α$, свя­зан­но­му с чис­лом $k$ со­от­но­ше­ни­ем $$\alpha = \frac{2}{\sqrt{2\pi }}\int_{k}^{\infty }e^{-x^2/2}dx.$$

Во­прос о ра­цио­наль­ном вы­бо­ре уров­ня зна­чи­мо­сти в дан­ных кон­крет­ных ус­ло­ви­ях (напр., при раз­ра­бот­ке пра­вил ста­ти­стич. кон­тро­ля ка­че­ст­ва мас­со­вой про­дук­ции) яв­ля­ет­ся весь­ма су­ще­ст­вен­ным. При этом же­ла­нию при­ме­нять пра­ви­ла лишь с вы­со­ким (близ­ким к еди­ни­це) уров­нем зна­чи­мо­сти про­ти­во­сто­ит то об­стоя­тель­ст­во, что при ог­ра­ни­чен­ном чис­ле на­блю­де­ний та­кие пра­ви­ла по­зво­ля­ют сде­лать лишь очень бед­ные вы­во­ды (напр., не да­ют воз­мож­но­сти ус­та­но­вить раз­ли­чие ве­ро­ят­но­стей двух со­бы­тий да­же при за­мет­ном раз­ли­чии час­тот этих со­бы­тий).

Дальнейшие задачи математической статистики

В упо­ми­нав­ших­ся вы­ше за­да­чах оцен­ки па­ра­мет­ров и про­вер­ки ги­по­тез ис­поль­зу­ет­ся пред­по­ло­же­ние, что чис­ло на­блю­де­ний, не­об­хо­ди­мых для дос­ти­же­ния за­дан­ной точ­но­сти вы­во­дов, оп­ре­де­ля­ют за­ра­нее (до про­ве­де­ния ис­пы­та­ний). Од­на­ко час­то ап­ри­ор­ное оп­ре­де­ле­ние чис­ла на­блю­де­ний не­це­ле­со­об­раз­но, т. к., не фик­си­руя чис­ло опы­тов за­ра­нее, а оп­ре­де­ляя его в хо­де экс­пе­ри­мен­та, мож­но умень­шить ма­те­ма­тич. ожи­да­ние чис­ла не­об­хо­ди­мых на­блю­де­ний. Сна­ча­ла это об­стоя­тель­ст­во бы­ло под­ме­че­но на при­ме­ре вы­бо­ра од­ной из двух ги­по­тез ($H_1$ или $H_2$) по по­сле­до­ватель­но­сти не­за­ви­си­мых ис­пы­та­ний. Со­от­вет­ст­вую­щая про­це­ду­ра (впер­вые пред­ло­жен­ная в свя­зи с за­да­ча­ми при­ё­моч­но­го ста­ти­сти­че­ско­го кон­тро­ля) со­сто­ит в сле­дую­щем. На ка­ж­дом ша­ге по ре­зуль­та­там уже про­ве­дён­ных на­блю­де­ний ре­ша­ют а) про­вес­ти сле­дую­щее ис­пы­та­ние, или б) пре­кра­тить ис­пы­та­ния и при­нять ги­по­те­зу $H_1$, или в) пре­кра­тить ис­пы­та­ния и при­нять ги­по­те­зу $H_2$. При над­ле­жа­щем под­бо­ре ко­ли­че­ст­вен­ных ха­рак­те­ри­стик по­доб­ной про­це­ду­ры мож­но до­бить­ся (при той же точ­но­сти вы­во­дов) со­кра­ще­ния чис­ла на­блю­де­ний в ср. поч­ти вдвое по срав­не­нию с про­це­ду­рой, ис­поль­зую­щей вы­бор­ки фик­си­ров. объ­ё­ма (см. По­сле­до­ва­тель­ный ана­лиз). Раз­ви­тие ме­то­дов по­сле­до­ва­тель­но­го ана­ли­за при­ве­ло, с од­ной сто­ро­ны, к изу­че­нию управ­ляе­мых слу­чай­ных про­цес­сов, с др. – к по­яв­ле­нию об­щей тео­рии ста­ти­сти­че­ских ре­ше­ний. Эта тео­рия ис­хо­дит из то­го, что ре­зуль­та­ты по­сле­до­ва­тель­но про­во­ди­мых на­блю­де­ний слу­жат ос­но­вой при­ня­тия не­ко­то­рых ре­ше­ний (про­ме­жу­точ­ных – про­дол­жать ис­пы­та­ния или нет, и окон­ча­тель­ных – в слу­чае пре­кра­ще­ния ис­пы­та­ний). В за­да­чах оцен­ки па­ра­мет­ров окон­чат. ре­ше­ния суть чис­ла (зна­че­ние оце­нок), в за­да­чах про­вер­ки ги­по­тез – при­ни­мае­мые ги­по­те­зы. Цель тео­рии – ука­зать пра­вила при­ня­тия ре­ше­ний, ми­ни­ми­зи­рую­щих ср. риск или убы­ток (риск за­ви­сит и от ве­ро­ят­но­ст­ных рас­пре­де­ле­ний ре­зуль­та­тов на­блю­де­ний, и от при­ни­мае­мо­го окон­чат. ре­ше­ния, и от рас­хо­дов на про­ве­де­ние ис­пы­та­ний).

Во­про­сы це­ле­со­об­раз­но­го рас­пре­де­ле­ния уси­лий при про­ве­де­нии ста­ти­стич. ана­ли­за яв­ле­ний рас­смат­ри­ва­ют­ся в тео­рии пла­ни­ро­ва­ния экс­пе­ри­мен­та, став­шей важ­ной ча­стью совр. ма­те­ма­тич. ста­ти­сти­ки.

На­ря­ду с раз­ви­ти­ем и уточ­не­ни­ем об­щих по­ня­тий М. с. раз­ви­ва­ют­ся и её отд. раз­де­лы, та­кие как дис­пер­си­он­ный ана­лиз, кор­ре­ля­ци­он­ный ана­лиз, мно­го­мер­ный ста­ти­сти­че­ский ана­лиз, ста­ти­сти­че­ский ана­лиз слу­чай­ных про­цес­сов, рег­рес­си­он­ный ана­лиз, фак­тор­ный ана­лиз.

Ис­то­ри­че­ская справ­ка. Пер­вые за­да­чи М. с. поя­ви­лись в тру­дах Я. Бер­нул­ли, П. Ла­п­ла­са и С. Пу­ас­со­на. В Рос­сии ме­то­ды М. с. в при­ме­не­нии к де­мо­гра­фии и стра­хо­во­му де­лу раз­ви­вал на ос­но­ве тео­рии ве­ро­ят­но­стей В. Я. Бу­ня­ков­ский (1846). Ре­шаю­щее зна­че­ние для даль­ней­ше­го раз­ви­тия М. с. име­ли ра­бо­ты пред­ста­ви­те­лей рос. шко­лы тео­рии ве­ро­ят­но­стей 2-й пол. 19 – нач. 20 вв. (П. Л. Че­бы­шев, А. А. Мар­ков, А. М. Ля­пу­нов, С. Н. Берн­штейн). Мн. во­про­сы тео­рии ста­ти­стич. оце­нок бы­ли по су­щест­ву раз­ра­бо­та­ны на ос­но­ве тео­рии оши­бок и ме­то­да наи­мень­ших квад­ра­тов (К. Га­усс и А. А. Мар­ков). Тру­ды А. Кет­ле, Ф. Галь­то­на и К. Пир­со­на име­ли боль­шое зна­че­ние, но по уров­ню ис­поль­зо­ва­ния дос­ти­же­ний тео­рии ве­ро­ят­но­стей от­ста­ва­ли от ра­бот рос. шко­лы. Пир­со­ном бы­ла ши­ро­ко раз­вёр­ну­та ра­бо­та по со­став­ле­нию таб­лиц функ­ций, не­об­хо­ди­мых для при­ме­не­ния ме­то­дов М. с. Она бы­ла про­дол­же­на во мн. на­уч. цен­трах (в СССР она ве­лась Е. Е. Слуц­ким, Н. В. Смир­но­вым, Л. Н. Боль­ше­вым). В соз­да­нии тео­рии ма­лых вы­бо­рок, об­щей тео­рии ста­ти­стич. оце­нок, про­вер­ки ги­по­тез (ос­во­бо­ж­дён­ной от пред­по­ло­же­ний о на­ли­чии ап­ри­ор­ных рас­пре­де­ле­ний), по­сле­до­ва­тель­но­го ана­ли­за зна­чи­тель­на роль пред­ста­ви­те­лей анг­ло-амер. шко­лы [Стью­дент (псевд. У. Гос­се­та), Р. Фи­шер, Э. Пир­сон, Ю. Ней­ман, А. Вальд], дея­тель­ность ко­то­рых на­ча­лась в 1-й четв. 20 в. В СССР зна­чит. ре­зуль­та­ты в об­лас­ти М. с. по­лу­че­ны А. Н. Кол­мо­го­ро­вым, В. И. Ро­ма­нов­ским, Слуц­ким, ко­то­ро­му при­над­ле­жат важ­ные ра­бо­ты по ста­ти­сти­ке ста­цио­нар­ных ря­дов, Смир­но­вым, за­ло­жив­шим ос­но­вы тео­рии не­па­ра­мет­рич. ме­то­дов М. с., Ю. В. Лин­ни­ком, обо­га­тив­шим ана­ли­тич. ап­па­рат М. с. но­вы­ми ме­то­да­ми. На ос­но­ве М. с. ин­тен­сив­но раз­ра­ба­ты­ва­ют­ся ста­ти­стич. ме­то­ды ис­сле­до­ва­ния и кон­тро­ля мас­со­во­го про­из­вод­ст­ва, ста­ти­стич. ме­то­ды в об­лас­ти фи­зи­ки, гид­ро­ло­гии, кли­ма­то­ло­гии, звёзд­ной ас­тро­но­мии, био­ло­гии, ме­ди­ци­ны и др.