КРА́ТНЫЙ ИНТЕГРА́Л
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
КРА́ТНЫЙ ИНТЕГРА́Л, интеграл от функции многих переменных $f(x_1,...,x_m), m⩾ 2$, взятый по области $m$-мерного пространства. При $m=2$ К. и. называют двойным интегралом, при $m=3$ – тройным.
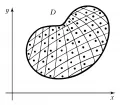
Характерным примером являются двойные интегралы. Пусть функция $f(x,y)$ задана в квадрируемой области $D$ на плоскости. Область $D$ разбивают на $n$ частичных областей $d_i$, которые имеют площади $s_i$. В каждой области $d_i$ произвольным образом выбирается (см. рис.) точка $(x_i,y_i)$ и составляется интегральная сумма $$S_n=\sum_{i=1}^nf(x_i,y_i)s_i.$$Если при неограниченном уменьшении макс. диаметра областей $d_i, i=1,...,n$, суммы $S_n$ имеют предел, не зависящий от выбора областей $d_i$ и точек $(x_i,y_i)$, то этот предел называют двойным интегралом от функции $f(x,y)$ по области $D$ и обозначают $$\iint_{D}f(x,y)ds,$$ Если функция $f$ непрерывна и область $D$ замкнута, то интеграл заведомо существует. Аналогично определяются тройной интеграл и вообще $m$-кратные интегралы.
На К. и. переносятся мн. свойства интеграла Римана по отрезку (линейность, аддитивность относительно области интегрирования, возможность интегрирования неравенств и др.). Вместе с тем интегрируемая функция многих переменных может быть и неограниченной на $D$.
Для вычисления К. и. их обычно сводят к интегралам от меньшего числа переменных (см. Повторный интеграл). Для приближённого вычисления используют т. н. кубатурные формулы.
К. и. имеют разл. применения, с их помощью выражаются объёмы и массы тел, статич. моменты, моменты инерции и т. п.
