АСИ́МПТОТА

Рис. 2.

Рис. 1.

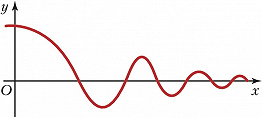
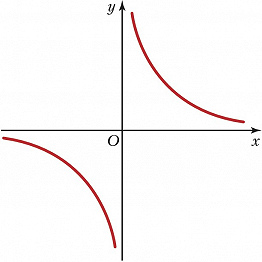
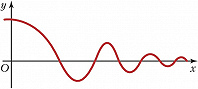
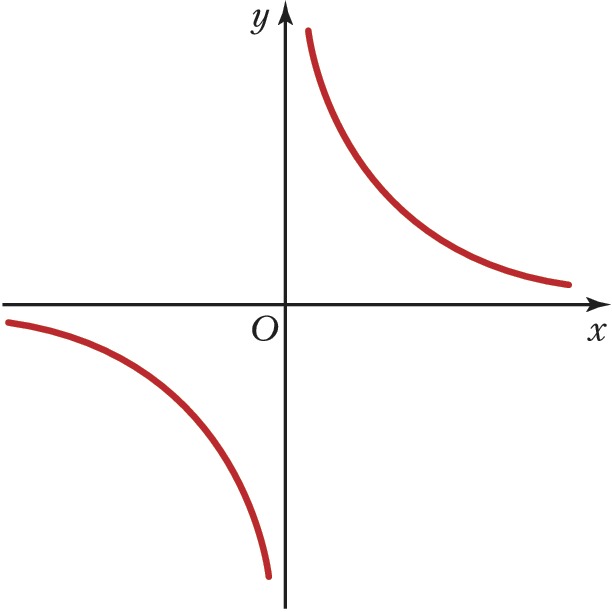
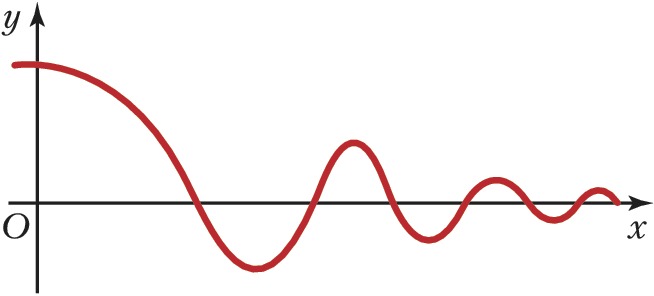
АСИ́МПТОТА (от греч. ἀσύμπτωτος – несов­па­даю­щий, не ка­саю­щий­ся) кри­вой с бес­ко­неч­ной вет­вью, пря­мая, к ко­то­рой эта ветвь не­ог­ра­ни­чен­но при­бли­жа­ет­ся; напр., для ги­пер­бо­лы $y=1/x$ (рис. 1) асим­пто­та­ми яв­ля­ют­ся оси ко­ор­ди­нат $Ox$ и $Oy$. Кри­вая мо­жет пе­ре­секать свою А. (напр., гра­фик за­ту­хающих ко­ле­ба­ний на рис. 2). Кри­вые с бес­ко­неч­ны­ми вет­вя­ми мо­гут не иметь А. (напр., у па­ра­бо­лы нет А.). Ес­ли гра­фик функ­ции $y=f(x)$ при $x→∞$ име­ет А., оп­ре­де­ляе­мую урав­не­ни­ем $y=ax+b$, то эта функ­ция мо­жет быть пред­ставлена в ви­де $f(x)=ax+b+α(x)$, где $α(x)→0$ при $x→∞$.

Тер­мин «А.» (при­ме­ни­тель­но к ги­пер­бо­ле) при­пи­сы­ва­ют Апол­ло­нию Перг­ско­му.