ЛЕ́РНЕРА И́НДЕКС

ЛЕ́РНЕРА И́НДЕКС, по­ка­за­тель ры­ноч­ной вла­сти мо­но­по­ли­ста; ха­рак­те­ри­зу­ет от­но­си­тель­ную раз­ни­цу ме­ж­ду мо­но­поль­ной це­ной и пре­дель­ны­ми из­держ­ка­ми про­из­вод­ст­ва. Пред­ло­жен А. Лер­не­ром в 1934.$$I_{L}=\frac{P_{m}-MC}{P_{m}}=\frac{1}{E},$$где $I_L$ – ин­декс мо­но­поль­ной вла­сти Лер­не­ра, $P_m$ – мо­но­поль­ная це­на, $MC$ – пре­дель­ные из­держ­ки, $E$ – эла­стич­ность спро­са на про­дук­цию.

Со­глас­но Л. и., мо­но­поль­ная власть яв­ля­ет­ся ве­ли­чи­ной, об­рат­ной эла­стич­но­сти спро­са на про­дук­цию фир­мы ($1/E$).

Рис. 1. Монопольная власть в условиях эластичного спроса.

Рис. 2. Монопольная власть в условиях неэластичного спроса.

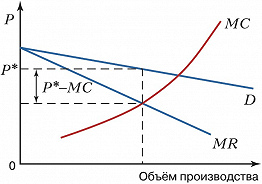
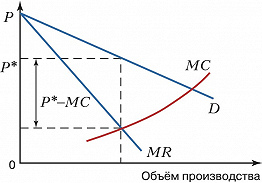
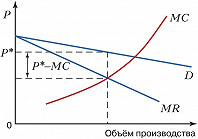
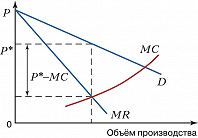
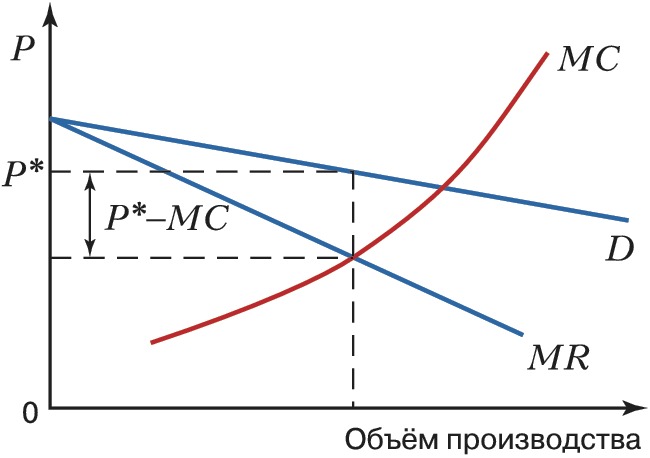
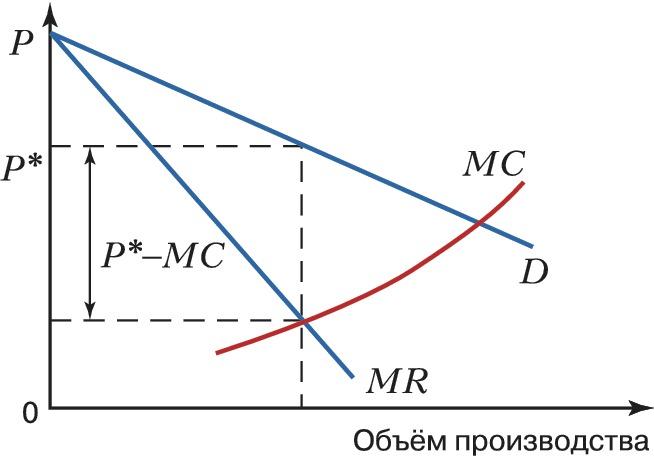
В ус­ло­ви­ях эла­стич­но­го спро­са и боль­шо­го ко­ли­че­ст­ва то­ва­ров-суб­сти­ту­тов от­но­си­тель­ная над­бав­ка к пре­дель­ным из­держ­кам не­ве­ли­ка (рис. 1). В ус­ло­ви­ях со­вер­шен­ной кон­ку­рен­ции (ко­гда эла­стич­ность спро­са стре­мит­ся к бес­ко­неч­но­сти и спрос пред­став­ля­ет го­ри­зон­таль­ную ли­нию) $MC=P$. Сле­до­ва­тель­но, $(P_m-MC)=0\; и\; I_L=0$. Ес­ли $I_L$ по­ло­жи­тель­ная ве­ли­чи­на ($I_L>0$), то фир­ма об­ла­да­ет мо­но­поль­ной вла­стью. Чем вы­ше этот по­ка­за­тель, тем боль­ше мо­но­поль­ная власть (рис. 2). Она мак­си­маль­на при эла­стич­но­сти рав­ной 0.

Вы­чис­лить Л. и. не­про­сто в свя­зи с труд­но­стью рас­чё­та ре­аль­ных пре­дель­ных из­дер­жек. По­это­му на прак­ти­ке пре­дель­ные из­держ­ки за­ме­ня­ют сред­ни­ми ($AC$). В этом слу­чае ис­ход­ная фор­му­ла мо­жет быть за­пи­са­на:$$I_{L}=\frac{P-AC}{P}.$$

.

Ес­ли ум­но­жить чис­ли­тель и зна­ме­на­тель на объ­ём про­из­вод­ст­ва $Q$, то по­лу­чим в чис­ли­те­ле при­быль, а в зна­ме­на­те­ле – со­во­куп­ный (ва­ло­вой) до­ход:$$I_{L}=\frac{(P-AC)\cdot Q}{PQ}=\frac{\pi}{TR}. $$

Тем са­мым Л. и. рас­смат­ри­ва­ет вы­со­кие при­бы­ли как при­знак мо­но­по­лии. В из­вест­ной ме­ре это спра­вед­ли­во, од­на­ко бы­ва­ют слу­чаи, ко­гда вы­со­кая нор­ма при­бы­ли не яв­ля­ет­ся од­но­знач­ным при­зна­ком мо­но­по­лии. Это слу­ча­ет­ся, ко­гда ве­ли­ки раз­ли­чия ме­ж­ду бух­гал­тер­ской и эко­но­мич. при­бы­лью, т. е. ес­ли не учи­ты­ва­ют­ся за­тра­ты на соб­ст­вен­ный ка­пи­тал, осо­бен­но в ка­пи­та­ло­ём­ких от­рас­лях, оп­ла­та пред­при­ни­ма­тель­ских спо­соб­но­стей ус­пеш­но функ­цио­ни­рую­ще­го биз­нес­ме­на, опе­ра­ции с вы­со­кой сте­пенью рис­ка.

Для ха­рак­те­ри­сти­ки мо­но­поль­ной вла­сти ис­поль­зу­ет­ся и по­ка­за­тель, оп­ре­де­ляю­щий сте­пень кон­цен­тра­ции рын­ка, – Хер­фин­да­ля – Хирш­ма­на ин­декс $(I_{\text {HH}})$. При его рас­чё­те ис­поль­зу­ют­ся дан­ные об удель­ном ве­се про­дук­ции фир­мы в от­рас­ли.