ДЖИ́НИ КОЭФФИЦИЕ́НТ
-
Рубрика: Экономика
-
-
Скопировать библиографическую ссылку:
ДЖИ́НИ КОЭФФИЦИЕ́НТ, показатель, используемый в статистике для оценки степени концентрации изучаемого признака или неравномерности его распределения по единицам или группам единиц совокупности статистической. Сосредоточение относительных объёмов признака у отд. единиц соответственно приводит к пропорциональному уменьшению относительных объёмов у единиц оставшейся части совокупности, что и вызывает неравномерность распределения. Такая неравномерность может иметь место в распределении доходов по группам населения, трудовых ресурсов по регионам страны, активов по кредитным организациям и т. п. Наряду с термином «концентрация» в конкретных предметных областях используются и др. термины, напр. «локализация» или «дифференциация».
Расчёт Д. к. базируется на использовании кривой концентрации (кривая Лоренца). Для её построения необходимо иметь частотное распределение единиц исследуемой совокупности и взаимосвязанное с ним частотное распределение изучаемого признака. При этом для удобства вычислений и повышения аналитичности данных единицы совокупности, по возможности, разбивают на равные группы: 10 групп – по 10% единиц в каждой или 5 групп – по 20% единиц. Так, напр., в практике статистики при изучении дифференциации населения по доходам выделяют 5 групп по степени их увеличения: первая – с наименьшими доходами, пятая – с наибольшими.
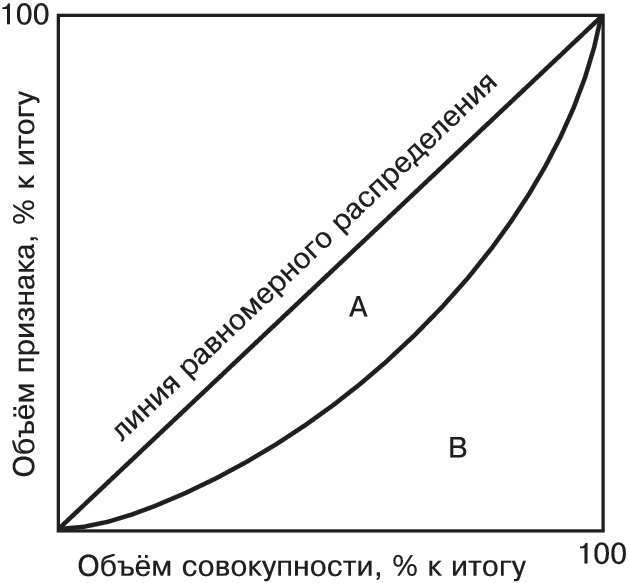
Кривая Лоренца строится в прямоугольной системе координат. На оси абсцисс откладываются накопленные частоты объёма совокупности, а на оси ординат – накопленные частоты объёма признака. Полученная кривая и будет характеризовать степень концентрации.
Если распределение является строго равномерным, то первые 20% единиц ранжированной совокупности (населения) обладают 20% объёма признака (совокупных доходов), первые 40% единиц – соответственно 40% объёма признака и т. д. Такое распределение отображается прямой, проходящей из нижнего левого угла графика к верхнему правому углу и являющейся линией равномерного распределения. Чем сильнее концентрация изучаемого признака, тем заметнее кривая Лоренца отклоняется вниз от линии равномерного распределения, и наоборот, чем слабее концентрация, тем ближе будет кривая к прямой.
Степень концентрации (рис.) определяется площадью фигуры А, ограниченной линией равномерного распределения и кривой Лоренца. Чем больше площадь А и чем соответственно меньше площадь В, тем степень концентрации выше. На сравнении площади А с площадью треугольника, расположенного ниже линии равномерного распределения, основан Д. к., расчётная формула которого имеет вид: $$G=1-2 \displaystyle \sum_{i=1}^k \boldsymbol d_{xi} \boldsymbol d^H_{yi} + \displaystyle \sum_{i=1}^k \boldsymbol d_{xi} \boldsymbol d_{yi},$$где $\boldsymbol d_{xi}$ – доля $i$-й группы в общем объёме совокупности; $\boldsymbol d_{yi}$ – доля $i$-й группы в общем объёме признака; $\boldsymbol d_{yi}^H$ – накопленная доля $i$-й группы в общем объёме признака.
Интервал принимаемых Д. к. значений – от 0 до 1. По данным Федеральной службы гос. статистики, Д. к., характеризующий дифференциацию населения России по доходам, в 1995 составлял 0,387, а в 2004 – 0,407. В РФ Д. к. стал применяться лишь с 1990-х гг., и как во время экономич. кризиса 1990-х гг., так и в период экономич. роста 2000-х гг. показывал низкую эгалитарность (от франц. égalité – равенство) рос. общества.