РАСТВО́РЫ

РАСТВО́РЫ, го­мо­ген­ные (од­но­род­ные) сис­те­мы, со­стоя­щие из двух или бо­лее ком­по­нен­тов и воз­мож­ных про­дук­тов их взаи­мо­дей­ст­вия. Р. пред­став­ля­ют со­бой фа­зы пе­ре­мен­но­го со­ста­ва. Раз­ли­ча­ют га­зо­об­раз­ные, твёр­дые (см. Твёр­дые рас­тво­ры) и жид­кие Р. Воз­дух пред­став­ля­ет со­бой Р., на­хо­дя­щий­ся в га­зо­об­раз­ном со­стоя­нии. При­ме­ром твёр­до­го Р. мо­жет слу­жить сплав се­реб­ра с зо­ло­том, ис­поль­зуе­мый юве­ли­ра­ми для из­го­тов­ле­ния ук­ра­ше­ний. Жид­кие Р. – чай, со­ки, пить­е­вая во­да, бен­зин и мн. др.

Тер­мин «Р.» ча­ще от­но­сят к жид­ким Р. Ве­ще­ст­во, ко­то­рое на­хо­дит­ся при рас­смат­ри­вае­мой темп-ре в том же аг­ре­гат­ном со­стоя­нии, что и Р., и ко­ли­че­ст­вен­но в нём пре­об­ла­да­ет, при­ня­то на­зы­вать рас­тво­ри­те­лем. Ес­ли один из ком­по­нен­тов Р. в чис­том ви­де при рас­смат­ри­вае­мой темп-ре яв­ля­ет­ся жид­ко­стью, а дру­гой – га­зом или твёр­дым ве­ще­ст­вом, то пер­вый ком­по­нент на­зы­ва­ют рас­тво­ри­те­лем, а вто­рой – рас­тво­рён­ным ве­ще­ст­вом. В за­ви­си­мо­сти от при­ро­ды рас­тво­ри­те­ля жид­кие Р. мо­гут быть вод­ны­ми и не­вод­ны­ми (спир­то­вые, ам­ми­ач­ные и т. п.). Ко­ли­че­ст­во рас­тво­рён­но­го ве­ще­ст­ва, на­хо­дя­ще­го­ся в дан­ном ко­ли­че­ст­ве Р. или рас­тво­ри­те­ля, на­зы­ва­ют кон­цен­тра­ци­ей Р. Наи­бо­лее час­то ис­поль­зуе­мые спо­со­бы вы­ра­же­ния кон­цен­тра­ции сле­дую­щие: мас­со­вая до­ля $w_i=g_i/\sum g_i$ ($g_i$ – мас­са $i$-го ве­ще­ст­ва); моль­ная до­ля $x_i=n_i/\sum n_i$ ($n_i$ – ко­ли­че­ст­во $i$-го ве­ще­ст­ва в мо­лях); мо­ляль­ность $m_i$ – ко­ли­че­ст­во $i$-го ком­по­нен­та в мо­лях на 1000 г рас­тво­ри­те­ля $m_i=1000n_i/g_i$; мо­ляр­ность $c_i$ – ко­ли­че­ст­во $i$-го ком­по­нен­та в мо­лях на 1 дм³ рас­тво­ра $c_i=n_i/V$ ($V$ – объ­ём рас­тво­ра в дм³). В за­ви­си­мо­сти от кон­цен­тра­ции рас­тво­рён­но­го ве­ще­ст­ва Р. под­раз­де­ля­ют на кон­цен­три­ро­ван­ные и раз­бав­лен­ные.

Р., на­хо­дя­щий­ся при дан­ных ус­ло­виях (темп-ра, дав­ле­ние) в рав­но­ве­сии с рас­тво­рён­ным ве­ще­ст­вом, на­зы­ва­ют на­сы­щен­ным. Мас­су ве­ще­ст­ва, при­хо­дя­ще­го­ся на 100 г рас­тво­ри­те­ля в на­сы­щен­ном Р., на­зы­ва­ют рас­тво­ри­мо­стью. Рас­тво­ри­мость мн. ве­ществ силь­но за­ви­сит от темп-ры. При ох­ла­ж­де­нии вод­ных Р. не­ко­то­рые со­ли вы­де­ля­ют­ся в ви­де кри­стал­ло­гид­ра­тов, со­дер­жа­щих мо­ле­ку­лы во­ды. При на­гре­ва­нии эти ве­ще­ст­ва по­с­те­пен­но те­ря­ют во­ду, пре­вра­ща­ясь в без­вод­ные со­ли. Напр., при темп-ре вы­ше 45 °С из на­сы­щен­но­го Р. хло­ри­да каль­ция кри­стал­ли­зу­ет­ся ди­гид­рат CaCl₂·2H₂O, в ин­тер­ва­ле 30–45 °С – тет­ра­гид­рат CaCl₂·4H₂O, ни­же 30 °С – гек­са­гид­рат CaCl₂·6H₂O; для по­лу­че­ния без­вод­ной со­ли не­об­хо­ди­мо на­греть кри­стал­ло­гид­рат до 260 °С.

За­да­чи тео­рии Р. – свя­зать свой­ст­ва Р. со свой­ст­ва­ми мо­ле­кул или с мак­ро­ско­пич. свой­ст­ва­ми чис­тых ком­по­нен­тов. Стро­гое ре­ше­ние пер­вой за­да­чи воз­мож­но ме­то­да­ми ста­ти­стич. фи­зи­ки жид­ко­го со­стоя­ния. Для это­го не­об­хо­ди­мо знать по­тен­ци­ал пар­но­го взаи­мо­дей­ст­вия мо­ле­кул. Од­на­ко по­тен­ци­ал меж­мо­ле­ку­ляр­но­го взаи­мо­дей­ст­вия из­вес­тен или мо­жет быть рас­счи­тан лишь для про­стых мо­ле­кул. По­это­му ис­поль­зу­ют мо­дель­ные фор­мы по­тен­циа­ла, а час­то так­же мо­дель­ные пред­став­ле­ния о струк­ту­ре Р. (мо­де­ли ре­шё­точ­ная, ячеи­стая, сво­бод­но­го объ­ё­ма и др.). Рас­чё­ты мак­ро­ско­пич. свойств на ос­но­ве по­сту­ли­руе­мых мо­де­лей и срав­не­ние их с экс­пе­рим. дан­ны­ми для ре­аль­ных Р. по­зво­ля­ют вы­явить наи­бо­лее аде­к­ват­ные мо­де­ли и со­вер­шен­ст­во­вать тео­ре­тич. пред­став­ле­ния. Тер­мо­ди­на­мич. тео­рия Р. ста­вит пе­ред со­бой бо­лее скром­ные за­да­чи: рас­чёт по опыт­ным дан­ным тер­мо­ди­на­мич. функ­ций при из­ме­не­нии со­ста­ва и вы­чис­ле­ния од­них тер­мо­ди­на­мич. функ­ций, ес­ли из­вест­ны дру­гие.

Для отд. рас­смот­ре­ния име­ет смысл вы­де­лить Р. не­элек­тро­ли­тов, элек­тро­ли­тов, по­ли­ме­ров (см. Рас­тво­ры по­ли­ме­ров) и кол­ло­ид­ные Р., свой­ст­ва ко­то­рых су­ще­ст­вен­но раз­лич­ны. В даль­ней­шем тео­ре­тич. опи­са­нии свойств Р. бу­дем ис­поль­зо­вать фраг­мен­ты тер­мо­ди­на­мич. тео­рии.

Растворы неэлектролитов

Рис. 1. Смесь двух структурно подобных жидкостей ведёт себя как идеальный раствор.

В Р. не­элек­тро­ли­тов от­сут­ст­ву­ет элек­тро­ли­ти­че­ская дис­со­циа­ция мо­ле­кул на ио­ны, а меж­мо­ле­ку­ляр­ные взаи­мо­дей­ст­вия в чис­тых жид­ко­стях и в Р. близ­ки по при­ро­де и ин­тен­сив­но­сти. В ос­но­ве тер­мо­ди­на­мич. тео­рии Р. не­элек­тро­ли­тов ле­жит за­кон, сфор­му­ли­ро­ван­ный в 1885 Ф. Рау­лем, – в раз­бав­лен­ных Р. от­но­си­тель­ное по­ни­же­ние дав­ле­ния па­ра рас­тво­ри­те­ля над Р. рав­но моль­ной до­ле рас­тво­рён­но­го ве­ще­ст­ва:$$\frac{p_1^0-p_1}{p_1^0}=x_2=1-x_1$$где $p_1$ – дав­ле­ние на­сы­щен­но­го па­ра ком­по­нен­та над Р., $p_1^0$ – дав­ле­ние на­сы­щен­но­го па­ра над чис­тым ком­по­нен­том, $x_1$ и $x_2$ – моль­ные до­ли рас­тво­ри­те­ля и рас­тво­рён­но­го ве­ще­ст­ва. По­лу­чен­ное вы­ра­же­ние мож­но пре­об­ра­зо­вать к ви­ду: $p_i=p_i^0x_i$. Об­щее дав­ле­ние па­ра над Р. рав­но сум­ме пар­ци­аль­ных дав­ле­ний $p_1$ и $p_2$:$p=p_1+p_2=p_1^0x_1+p_2^0x_2=p_1^0+(p_2^0-p_1^0)x_2$, т. е. дав­ле­ние па­ра ли­ней­но за­ви­сит от со­ста­вов Р. В 1890 рос. фи­зи­ко­хи­мик И. Ф. Шре­дер пред­ло­жил рас­смат­ри­вать Р., под­чи­няю­щие­ся за­ко­ну Рау­ля при всех кон­цен­тра­ци­ях, как не­ко­то­рый стан­дарт. В даль­ней­шем та­кие Р. по­лу­чи­ли на­зва­ние иде­аль­ных (со­вер­шен­ных) Р. (рис. 1). Под­чи­не­ние за­ко­ну Рау­ля эк­ви­ва­лент­но то­му, что хи­мич. по­тен­ци­ал ком­по­нен­та Р. $μ_i$ та­кой же, как и хи­мич. по­тен­ци­ал в сме­си иде­аль­ных га­зов: $μ_i=μ_i^0+RT\ln x_i$, где $μ_i^0$ – хи­мич. по­тен­ци­ал чис­то­го $i$-го ком­по­не­нта.

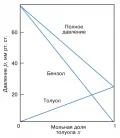Рис. 2. Изотермы давления пара в системе с положительными (I) и знакопеременными (II) отклонениями от закона Рауля.

С тер­мо­ди­на­мич. точ­ки зре­ния Р. яв­ля­ет­ся иде­аль­ным, ес­ли при его об­ра­зо­ва­нии не про­ис­хо­дит энер­ге­тич. из­ме­не­ний, а из­ме­ня­ет­ся толь­ко эн­тро­пия ком­по­нен­тов на ве­ли­чи­ну $ΔS_i=-R\ln x_i$. На ос­но­ве мо­дель­ных пред­став­ле­ний иде­аль­ный Р. мож­но оп­ре­де­лить как со­во­куп­ность ком­по­нен­тов, в ко­то­рой по­ве­де­ние ка­ж­дой мо­ле­ку­лы не за­ви­сит от со­ста­ва. Для би­нар­но­го Р. это ут­вер­жде­ние оз­на­ча­ет, что долж­ны быть оди­на­ко­вы по­тен­циа­лы пар­но­го взаи­мо­дей­ст­вия мо­ле­кул рас­тво­ри­те­ля $φ_{11}$, рас­тво­рён­но­го ве­ще­ст­ва $φ_{22}$ и их взаи­мо­дей­ст­вия друг с дру­гом $φ_{12}$, по­сколь­ку в этом слу­чае сме­ше­ние жид­ко­стей не со­про­во­ж­да­ет­ся энер­ге­тич. из­ме­не­ния­ми. Раз­ли­чия в по­тен­циа­лах $φ_{11}$, $φ_{22}$, $φ_{12}$ бу­дут при­во­дить к от­ри­ца­тель­но­му или по­ло­жи­тель­но­му от­кло­не­нию от за­ко­на Рау­ля. Напр., по­ло­жи­тель­ные от­кло­не­ния от иде­аль­но­сти вы­зы­ва­ют ас­со­циа­ции од­но­род­ных мо­ле­кул. Англ. хи­мик У. Ген­ри экс­пе­ри­мен­таль­но об­на­ру­жил, что в ре­аль­ных Р. при низ­кой кон­цен­тра­ции, ко­гда взаи­мо­дей­ст­вия $φ_{22}$ прак­ти­че­ски от­сут­ст­ву­ют, дав­ле­ние па­ра рас­тво­рён­но­го ве­ще­ст­ва так­же про­пор­цио­наль­но его моль­ной до­ле (Ген­ри за­кон), но ко­эф. про­пор­цио­наль­но­сти $K_Г$, по­лу­чив­ший назв. кон­стан­ты Ген­ри, от­ли­чен от дав­ле­ния па­ра чис­то­го ве­ще­ст­ва: $p_2=K_Гx_2$. Р., в ко­то­рых рас­тво­рён­ное ве­ще­ст­во под­чи­ня­ет­ся за­ко­ну Ген­ри, а рас­тво­ри­тель – за­ко­ну Рау­ля, на­зы­ва­ют пре­дель­но раз­бав­лен­ны­ми. На рис. 2 по­ка­за­ны об­лас­ти вы­пол­не­ния за­ко­нов Рау­ля и Ген­ри для би­нар­но­го рас­тво­ра, со­стоя­ще­го из ком­по­нен­тов А и В.

Рис. 3. Химический потенциал растворителя в присутствии растворённого вещества. Из-за различия в величинах углов, под которыми пересекаются линии (определяются энтропиями фаз), уменьшение химического ...

Свой­ст­ва раз­бав­лен­ных Р., со­дер­жа­щих не­ле­ту­чие ве­ще­ст­ва, за­ви­сят от при­ро­ды рас­тво­ри­те­ля, кон­цен­тра­ции рас­тво­рён­но­го ве­ще­ст­ва и не за­ви­сят от свойств час­тиц рас­тво­рён­но­го ве­ще­ст­ва. По­это­му их на­зы­ва­ют кол­ли­га­тив­ны­ми, до­слов­но – за­ви­ся­щи­ми от ко­ли­че­ст­ва. К ним от­но­сят­ся: по­ни­же­ние дав­ле­ния па­ра рас­тво­ри­те­ля над Р., по­ни­же­ние темп-ры за­мер­за­ния Р. по срав­не­нию с чис­тым рас­тво­ри­те­лем, по­вы­ше­ние тем­пе­ра­тур ки­пе­ния Р. по срав­не­нию с чис­тым рас­тво­ри­те­лем, ос­мо­тич. дав­ле­ние. При­чи­ной по­яв­ле­ния кол­ли­га­тив­ных свойств у Р. яв­ля­ет­ся умень­ше­ние хи­мич. по­тен­циа­ла рас­тво­ри­те­ля в при­сут­ст­вии рас­тво­рён­но­го ве­ще­ст­ва. Хи­мич. по­тен­ци­ал чис­той жид­ко­сти ра­вен $μ^0_1$, при до­бав­ле­нии вто­ро­го ком­по­нен­та он умень­ша­ет­ся до $μ^0_1+RT\ln x_1$, т. к. $x_1\lt 1$, а $\ln x_1\lt 0$. На зна­че­ние хи­мич. по­тен­циа­ла рас­тво­ри­те­ля в га­зо­вой или твёр­дой фа­зе рас­тво­рён­ное ве­ще­ст­во влия­ния не ока­зы­ва­ет, по­то­му что оно от­сут­ст­ву­ет в этих фа­зах. Из кол­ли­га­тив­ных свойств Р. мож­но оп­ре­де­лить мо­ле­ку­ляр­ную мас­су рас­тво­рён­но­го ве­ще­ст­ва. На рис. 3 при­ве­де­на тем­пе­ра­тур­ная за­ви­си­мость хи­мич. по­тен­циа­ла чис­то­го рас­тво­ри­те­ля и Р., из ко­то­рой вид­но по­ни­же­ние темп-ры за­мер­за­ния и по­вы­ше­ние темп-ры ки­пе­ния Р.

Для опи­са­ния свойств ре­аль­ных Р. вво­дят по­ня­тие ак­тив­но­сти $a_i$: $\ln a_i=\frac{μ_i-μ^0_i}{RT}$. Ес­ли пар над Р. ве­дёт се­бя как иде­аль­ный газ, то ак­тив­ность мож­но оп­ре­де­лить че­рез экс­пе­рим. из­меряемые ве­ли­чи­ны: $a_i=\frac{p_i}{p^0_i}$, где $p_i$ – давле­ние па­ра ве­ще­ст­ва над Р. – пар­ци­аль­ное дав­ле­ние, $p_i^0$ – дав­ле­ние па­ра над чис­тым рас­тво­ри­те­лем при той же темп-ре. Ак­тив­ность вы­ра­жа­ет­ся в ви­де про­из­ве­де­ния моль­ной до­ли на ко­эф. ак­тив­ности $γ$: $a_i=γ_ix_i$. С учё­том $a_i=\frac{p_i}{p_i^0}$ име­ем $γ_i=\frac{p_i}{x_ip_i^0}$. От­сю­да сле­ду­ет, что зна­че­ние $γ_i$ за­ви­сит от спо­со­ба вы­ра­же­ния кон­цен­тра­ции и вы­бо­ра стан­дарт­но­го со­стоя­ния.

В сим­мет­рич­ной сис­те­ме срав­не­ния стан­дарт­ным со­стоя­ни­ем яв­ля­ют­ся чис­тые ком­по­нен­ты при темп-ре Р. В асим­мет­рич­ной сис­те­ме срав­не­ния стан­дартным со­стоя­ни­ем рас­тво­ри­те­ля счи­та­ет­ся чис­тое ве­ще­ст­во, а для рас­тво­рён­но­го ве­ще­ст­ва – пре­дель­но раз­бав­лен­ный Р.

Для не­го $γ_2=\frac{p_2}{x_2 K_Γ}$. В слу­чае ре­аль­но­гоР.: $μ_i=μ_i^{cт}+RT\ln x_i+RT\ln γ_i=μ_i^{ид}+μ_i^E$, $μ_i^{cт}$ – хи­мич. по­тен­ци­ал в стан­дарт­ном со­стоя­нии, $μ_i^{ид}$ – хи­мич. по­тен­ци­ал идеаль­но­го Р., $μ_i^{E}=RT\ln γ_i$ – из­бы­точ­ный хи­мич. по­тен­ци­ал, от­ра­жаю­щий не­иде­аль­ность Р. В об­щем ви­де из­бы­точ­ную ве­ли­чи­ну оп­ре­де­ля­ют урав­не­ния­ми: $A^E=A(T,p,x)-A^{ид}(T,p,x)$. Ис­поль­зу­ют так­же функ­ции сме­ше­ния $A^M=A(T,p,x)-[x_1A_1^0+x_2A_2^0]$, где $A(T,p,x)$ – экс­тен­сив­ная тер­мо­ди­на­мическая ве­ли­чи­на (напр., эн­таль­пия, эн­тро­пия, энер­гия Гиб­бса, хи­мич. по­тен­ци­ал и др.), вто­рой член в урав­не­нии вы­ра­жа­ет функ­цию сме­ше­ния иде­аль­но­го Р. Объ­е­ди­няя, по­лу­чим: $A^E=A^M-A^{ид}$. Для важ­ней­шей тер­мо­ди­на­мич. функ­ции – энер­гии Гиб­бса – эти функ­ции име­ют вид: $G^E=RT[x_1\ln γ_1+(1-x_1)\ln γ_2]$ (из­бы­точная энер­гия Гиб­бса) и $G^M=RT[x_1\ln a_1+(1-x_1)\ln a_2]$ (энер­гия сме­ше­ния Гиб­бса).

Осн. за­да­ча тер­мо­ди­на­мич. тео­рии Р. – по­лу­чить ана­ли­тич. вы­ра­же­ние кон­цен­тра­ци­он­ной за­ви­си­мо­сти ко­эф. ак­тив­но­сти и из­бы­точ­ных функ­ций. Сре­ди не­иде­аль­ных Р. вы­де­ля­ют ре­гу­ляр­ные и атер­маль­ные. Для ре­гу­ляр­ных Р. эн­тро­пия сме­ше­ния сов­па­да­ет с эн­тро­пи­ей сме­ше­ния иде­аль­но­го Р., а един­ст­вен­ной при­чи­ной от­кло­не­ния от иде­аль­но­сти яв­ля­ет­ся на­ли­чие те­п­ло­ты сме­ше­ния. Ко­эф­фи­ци­ен­ты ак­тив­но­сти за­ви­сят от темп-ры $\ln γ_i\approx x_i^2/RT$. Для атер­маль­ных Р. те­п­ло­та сме­ше­ния рав­на ну­лю, но име­ет­ся из­бы­точ­ная эн­тро­пия сме­ше­ния. Ко­эф­фи­ци­ен­ты ак­тив­но­сти ком­по­нен­тов не за­ви­сят от темп-ры. Ре­гу­ляр­ные и атер­маль­ные Р. пред­став­ля­ют со­бой два пре­дель­ных слу­чая от­кло­не­ния от иде­аль­но­сти и, стро­го го­во­ря, в при­ро­де не су­ще­ст­ву­ют. Од­на­ко тео­рия ре­гу­ляр­ных и атер­маль­ных Р. в не­ко­то­рых слу­ча­ях по­зво­ля­ет при­бли­жён­но оха­рак­те­ри­зо­вать тер­мо­ди­на­мич. свой­ст­ва кон­крет­ных не­иде­аль­ных сис­тем.

Растворы электролитов

В элек­тро­ли­тов рас­тво­рах в ре­зуль­та­те элек­тро­ли­тич. дис­со­циа­ции мо­ле­кул рас­тво­рён­но­го ве­ще­ст­ва об­ра­зу­ют­ся ка­тио­ны и анио­ны. Рас­тво­ри­тель обыч­но прак­ти­че­ски не дис­со­ции­ро­ван. Сте­пень дис­со­циа­ции за­ви­сит от си­лы свя­зи ме­ж­ду ка­тио­на­ми и анио­на­ми в мо­ле­ку­ле элек­тро­ли­та, от ди­элек­трич. про­ни­цае­мо­сти рас­тво­ри­теля и его спо­соб­но­сти соль­ва­ти­ро­вать ио­ны. Ве­ще­ст­ва, со­дер­жа­щие ио­ны в ис­ход­ном со­стоя­нии, на­зы­ва­ют­ся ио­но­фо­ра­ми или ис­тин­ны­ми элек­тро­ли­та­ми; ве­ще­ст­ва, об­ра­зую­щие ио­ны при рас­тво­ре­нии, на­зы­ва­ют­ся ио­но­ге­на­ми или по­тен­ци­аль­ны­ми элек­тро­ли­та­ми. В мо­ле­ку­лах ио­но­фо­ров – ион­ная связь, ио­но­ге­нов – по­ляр­ная. В ка­че­ст­ве при­ме­ра при­ве­дём схе­му дис­со­циа­ции ио­но­ге­на $\ce{HCl}$ в во­де: $\ce{HCl + 5H2O ⇄ H3O+ + [Cl(H2O)4]-}$. Энер­гию раз­ры­ва свя­зи $\ce{H─Cl}$, рав­ную 432 кДж/моль, ком­пен­си­ру­ет те­п­ло­вой эф­фект ре­ак­ции гид­ра­та­ции ио­нов. Рас­смот­рим дис­со­циа­цию элек­тро­ли­та: $\ce{Μ_{ν+}A_{ν-} <=> ν_{+}Μ^{z+}+ν_{-}Α^{z-}}$. В си­лу элек­тро­ней­траль­но­сти Р. хи­мич. по­тен­ци­ал элек­тро­ли­та $μ_2$ свя­зан с хи­мич. по­тен­циа­ла­ми отд. ио­нов $μ_2=ν_{+}μ_{+}+ν_{-}μ_{-}$, а $μ_2$, $μ_{+}$, $μ_{-}$ свя­за­ны с ак­тив­но­стя­ми: $μ_2=μ_2^0+RT \ln a_2$, $μ_{+}=μ_{+}^0+RT\ln a_{+}$, $μ_{-}=μ_{-}^0+RT\ln a_{-}$.Учи­ты­вая, что элек­тро­ней­траль­ность со­блю­да­ет­ся и в стан­дарт­ном со­стоя­нии $μ_2^0=ν_{+}μ_{+}^0+ν_{-}μ_{-}^0$, по­лу­чим: $a_2=a_{+}^{ν_{+}}a_{-}^{ν_{-}}$.В свя­зи с тем, что ак­тив­ность отд. ио­нов нель­зя оп­ре­де­лить из экс­пе­ри­мен­та, вво­дят по­ня­тие ср. ак­тив­но­сти ио­нов – как ср. гео­мет­ри­че­ской из ак­тив­но­стей ио­нов, со­став­ляю­щих ис­сле­дуе­мый элек­тро­лит: $a_{\pm}=(a_{+}^{ν_{+}}a_{-}^{ν_{-}})^{1/ν}$, где $ν=ν_{+}+ν_{-}$. То­гда име­ем связь ме­жду экс­пе­ри­мен­таль­но оп­ре­де­ляе­мой ве­ли­чи­ной $a_2$ и ср. ак­тив­но­стью: $a_2=(a_{+}^{ν_{+}} a_{-}^{ν_{-}})=[(a_{+}^{ν_{+}} a_{-}^{ν_{-}})^{1/ν}]^ν=a^ν_{\pm}$. Ана­ло­гич­ным об­ра­зом вво­дят ср. ион­ный ко­эф. ак­тив­но­сти $γ_{±}$, ср. мо­ляль­ную кон­цен­тра­цию и ср. гео­мет­рич. сте­хио­мет­ри­че­ское чис­ло об­ра­зо­вав­ших­ся ка­тио­нов и анио­нов $ν_{±}$. Для рав­но­за­ряд­ных элек­тро­ли­тов ср. мо­ляль­ность рав­на об­щей мо­ляр­но­сти.

Су­ще­ст­ву­ет три спо­со­ба вы­ра­же­ния ак­тив­но­сти отд. ио­на $a_i$ че­рез про­из­ве­де­ние его кон­цен­тра­ции на ко­эф. ак­тив­но­сти с учё­том шка­лы кон­цен­тра­ций: $a_{im}=γ_{im}\frac{m_i}{m_i^0}$, $a_{ic}=γ_{ic}\frac{c_i}{c_i^0}$, $a_{ix}=f_{ix}x_i$, где $m_i$ – мо­ляль­ность (моль/кг рас­тво­ри­те­ля); $m_i^0$ – стан­дарт­ное зна­че­ние мо­ляль­но­сти, рав­ное 1 моль/кг; $c_i$ – мо­ля­р­ность (моль/дм³); $c_i^0$ – стан­дарт­ное зна­че­ние кон­цен­тра­ции, рав­ное 1 моль/дм³; $x_i$ – моль­ная до­ля рас­тво­рён­но­го ве­ще­ст­ва. Ко­эф­фи­ци­ен­ты по­лу­чи­ли на­зва­ния: $γ_{im}$ – мо­ляль­ный, $γ_{ic}$ – мо­ляр­ный, $f_{ix}$ – ра­циональ­ный. Ис­поль­зуя при­ве­дён­ные фор­му­лы, на­хо­дят со­от­но­ше­ние ср. мо­ляль­но­сти $m_±=ν_±m$, ср. ак­тив­но­сти $a_±m=ν_±γ_±m$ и ак­тив­но­сти элек­троли­та $a_2=ν_±^ν γ_±^ν m^ν$. За стан­дарт­ное со­стояние рас­тво­ри­те­ля в Р. силь­но­го элек­тро­ли­та вы­би­ра­ют чис­тый рас­тво­ри­тель, а для элек­тро­ли­та – ги­по­те­тич. Р. со ср. кон­цен­тра­ци­ей ио­нов элек­тро­ли­та, рав­ной еди­ни­це и со свой­ст­ва­ми пре­дель­но раз­бав­лен­но­го Р., у ко­то­ро­го от­сут­ст­ву­ют ион-ион­ные взаи­мо­дей­ст­вия. Ср. ко­эф. в раз­бав­лен­ном Р. элек­тро­ли­та мож­но оце­нить при по­мо­щи пра­ви­ла ион­ной си­лы. Ион­ная си­ла $I$ Р. силь­но­го элек­тро­ли­та в сме­си силь­ных элек­тро­ли­тов оп­ре­де­ля­ет­ся по урав­не­нию: $I=\frac{1}{2}\sum m_i z_i^2$ или $I=\frac{1}{2}\sum c_i z_i^2$, где $z_i$ – за­ряд ио­на. Со­глас­но пра­ви­лу ион­ной си­лы, в раз­бав­лен­ных Р. $γ_±$ за­ви­сит толь­ко от ион­ной си­лы Р. и не за­ви­сит от при­ро­ды др. ио­нов, на­хо­дя­щих­ся в Р. Пра­ви­ло спра­вед­ли­во при кон­цен­тра­ци­ях Р. до 0,01–0,02 моль/кг, но при­бли­жён­но им мож­но поль­зо­вать­ся до 0,1–0,2 моль/кг.

Тер­мо­ди­на­мич. под­ход ука­зы­ва­ет на спе­ци­фи­ку по­ве­де­ния Р. элек­тро­ли­тов, но не мо­жет объ­яс­нить осо­бен­но­сти это­го по­ве­де­ния. Элек­тро­ста­тич. тео­рия раз­бав­лен­ных Р. силь­ных элек­тро­ли­тов, раз­ви­тая в 1923 П. Де­ба­ем и Э. Хюк­ке­лем на ос­но­ве мо­дель­ных пред­став­ле­ний, по­зво­ля­ет вы­чис­лить ср. ко­эф. ак­тив­но­сти элек­тро­ли­та, эк­ви­ва­лент­ную элек­тро­про­вод­ность и тео­ре­ти­че­ски обос­но­вать пра­ви­ло ион­ной си­лы.

Ср. ко­эф. ак­тив­но­сти би­нар­но­го $z_{+}$, $z_{-}$-ва­лент­но­го элек­тро­ли­та мож­но рас­счи­тать по пре­дель­но­му за­ко­ну Де­бая – Хюк­ке­ля: $\lg γ_{\pm} = -|z_{+}z_{-}|A\sqrt I$, где $A=1,825·10^6(εT)^{–3/2} (моль^{–1}·кг)^{1/2}/К^{3/2}$. Су­ще­ст­ву­ют вто­рое и третье при­бли­же­ния за­ко­на Де­бая – Хюк­ке­ля, уточ­няю­щие по­ве­де­ние $γ_{±}$ с рос­том кон­цен­тра­ции элек­тро­ли­та.

Коллоидные растворы

К кол­ло­ид­ным от­но­сят­ся Р., в ко­то­рых рас­тво­рён­ное ве­ще­ст­во на­хо­дит­ся в ви­де час­тиц раз­ме­ром от 1 нм до 10 мкм. Та­кие час­ти­цы со­дер­жат от де­сят­ков до ты­сяч мо­ле­кул. В 1861 Т. Грэм об­на­ру­жил, что свой­ст­ва Р. же­ла­ти­ны, крах­ма­ла и др. ве­ществ силь­но от­ли­ча­ют­ся от свойств Р. не­ор­га­нич. со­еди­не­ний. При кон­цен­три­ро­ва­нии та­ких Р. кри­стал­ли­за­ция не про­ис­хо­дит, а вы­де­ля­ет­ся студ­не­об­раз­ная, клей­ко­вид­ная мас­са. Для кол­лои­дов ха­рак­тер­ны сла­бо вы­ра­жен­ная диф­фу­зия, низ­кое ос­мо­тич. дав­ле­ние, их Р. рас­сеи­ва­ют свет – луч, про­хо­дя­щий че­рез та­кой Р., ста­но­вит­ся ви­ди­мым сбо­ку (Тин­да­ля эф­фект). Даль­ней­шие ис­сле­до­ва­ния по­ка­за­ли, что та­ки­ми же свой­ст­ва­ми об­ла­да­ют сис­те­мы, об­ра­зо­ван­ные ти­пич­ны­ми кри­стал­лои­да­ми, ес­ли по­след­ние на­хо­дят­ся в сре­де не в ви­де мо­ле­кул, а в ви­де мель­чай­ших (дис­перс­ных) час­тиц. Так, хло­рид на­трия в во­де об­ра­зу­ет ис­тин­ный Р., а в ор­га­нич. жид­ко­стях – ти­пич­ный кол­ло­ид­ный Р. По­это­му сле­ду­ет го­во­рить не о кол­лои­дах и кри­стал­лои­дах, а о кол­ло­ид­ном (дис­перс­ном) со­стоя­нии ве­ще­ст­ва.

По­доб­но то­му как в ис­тин­ных Р. раз­ли­ча­ют рас­тво­рён­ное ве­ще­ст­во и рас­тво­ри­тель, кол­ло­ид­ные сис­те­мы рас­смат­ри­ва­ют как со­стоя­щие из дис­перс­ной фа­зы и дис­пер­си­он­ной сре­ды. Дис­перс­ные сис­те­мы мо­гут быть сво­бод­но- и связ­но­дис­перс­ны­ми. В сво­бод­но­дис­перс­ных сис­те­мах час­ти­цы обо­соб­ле­ны и уча­ст­ву­ют в те­п­ло­вом (бро­унов­ском) дви­же­нии; в связ­но­дис­перс­ных сис­те­мах час­ти­цы сце­п­ле­ны друг с дру­гом и об­ра­зу­ют про­стран­ст­вен­ную сет­ку. Дис­перс­ные сис­те­мы раз­ли­ча­ют по сте­пе­ни раз­дроб­лен­но­сти дис­перс­ной фа­зы. Дис­перс­ность оп­ре­де­ля­ют как от­но­ше­ние сум­мар­ной по­верх­но­сти раз­де­ла $S_{12}$ дис­перс­ной фа­зы 1 с дис­перс­ной фа­зой 2 к сум­мар­но­му объ­ё­му час­тиц $V$: $D=S_{12}/V_1∼1/r$. Ис­поль­зу­ют так­же удель­ную по­верх­ность $S_{yд}$ – от­но­ше­ние сум­мар­ной по­верх­ности раз­де­ла к об­щей мас­се час­тиц: $S_{yд}=S_{12}/m$. Из при­ве­дён­ных со­от­но­ше­ний сле­ду­ет: чем мень­ше раз­мер час­тиц $r$, тем вы­ше дис­перс­ность и боль­ше удель­ная по­верх­ность. По сте­пе­ни дис­перс­но­сти сис­те­мы де­лят на гру­бо­дис­перс­ные с $r\gt 1$ мкм и $S_{12}\lt 1$ м²/г и вы­со­ко­дис­перс­ные с $r\lt 1$ мкм и $S_{12}\gt 1$ м²/г.

Дис­перс­ные сис­те­мы мож­но так­же клас­си­фи­ци­ро­вать по аг­ре­гат­но­му со­стоя­нию дис­перс­ной фа­зы и дис­пер­си­он­ной сре­ды. Тип дис­перс­ной сис­те­мы при­ня­то обо­зна­чать дву­мя бу­к­ва­ми, пер­вая из ко­то­рых от­но­сит­ся к дис­перс­ной фа­зе, вто­рая – к дис­пер­си­он­ной сре­де. Бу­к­вы Т, Ж, Г обо­зна­ча­ют твёр­дое, жид­кое и га­зо­об­раз­ное со­стоя­ния. Сис­те­мы с жид­кой дис­пер­си­он­ной сре­дой – об­шир­ный класс дис­перс­ных сис­тем. Сю­да от­но­сят­ся раз­но­об­раз­ные сис­те­мы с твёр­дой дис­перс­ной фа­зой (тип Т/Ж) – зо­ли в слу­чае сво­бод­но­дис­перс­ных сис­тем и ге­ли в слу­чае связ­но­дис­перс­ных сис­тем. Про­то­плаз­ма жи­вых кле­ток, кровь, со­ки рас­те­ний – всё это зо­ли. В за­ви­симо­сти от раз­ме­ров час­тиц зо­ли од­но­го и то­го же ве­ще­ст­ва мо­гут иметь разл. ок­ра­ску, в от­ли­чие от ис­тин­ных Р., у ко­то­рых она оди­на­ко­вая. Напр., зо­ли зо­ло­та мо­гут быть зе­лё­ны­ми, си­ни­ми, фио­ле­то­вы­ми, виш­нё­вы­ми, ру­би­но­во-крас­ны­ми. Од­но из важ­ных свойств зо­лей – на­ли­чие на по­верх­но­сти час­тиц элек­трич. за­ря­дов од­но­го зна­ка вслед­ст­вие ад­сорб­ции кол­ло­ид­ны­ми час­ти­ца­ми ио­нов из Р. Для оса­ж­де­ния зо­ля не­об­хо­ди­мо, что­бы его час­ти­цы со­еди­ни­лись в бо­лее круп­ные аг­ре­га­ты. Этот про­цесс на­зы­ва­ет­ся коа­гу­ля­ци­ей, а оса­ж­де­ние час­тиц под дей­ст­ви­ем си­лы тя­же­сти – се­ди­мен­та­ци­ей. Коа­гу­ля­ция про­ис­хо­дит при при­бав­ле­нии к зо­лю Р. элек­тро­ли­та или др. зо­ля, час­ти­цы ко­то­ро­го име­ют про­ти­во­по­лож­ный за­ряд. При оп­ре­де­лён­ных ус­ло­ви­ях коа­гу­ля­ция зо­лей при­во­дит к об­ра­зо­ва­нию ге­лей. В этом слу­чае все кол­ло­ид­ные час­ти­цы, свя­зы­вая рас­тво­ри­тель, пе­ре­хо­дят в по­лу­жид­кое-по­лу­твёр­дое со­стоя­ние, спо­соб­ное удер­жи­вать фор­му. При­ме­ра­ми ге­лей яв­ля­ют­ся же­ле, мар­ме­лад, пас­ти­ла.

Сис­те­мы с жид­кой дис­перс­ной фа­зой Ж₁/Ж₂ – эмуль­сии, с га­зо­вой дис­перс­ной фа­зой Г/Ж – пе­ны. Сис­те­мы с га­зо­об­раз­ной дис­пер­си­он­ной сре­дой, объ­е­ди­няе­мые об­щим назв. аэ­ро­зо­ли, вклю­ча­ют ды­мы, пы­ли (Т/Г), ту­ма­ны (Ж/Г). Аэ­ро­золь, в ко­то­ром при­сут­ст­ву­ют жид­кие и твёр­дые час­ти­цы дис­перс­ной фа­зы (Т, Ж/Г), на­зы­ва­ют смо­гом. Дис­пер­сия­ми ти­па Г/Т яв­ля­ют­ся раз­но­об­раз­ные при­род­ные и ис­кусств. по­рис­тые ма­те­риа­лы (напр., ту­фы, пе­но­пла­сты, пе­но­бе­тон).

Дис­перс­ные сис­те­мы по ин­тен­сив­но­сти взаи­мо­дей­ст­вия ме­ж­ду фа­зой и сре­дой раз­де­ля­ют на лио­филь­ные и лио­фоб­ные. Для лио­филь­ных дис­перс­ных сис­тем ха­рак­тер­ны силь­ные взаи­мо­дей­ст­вия на меж­фаз­ной гра­ни­це. Та­кие сис­те­мы мо­гут об­ра­зо­вы­вать­ся пу­тём са­мо­про­из­воль­но­го дис­пер­ги­ро­ва­ния од­ной мак­ро­фа­зы в дру­гую и по­это­му яв­ля­ют­ся тер­мо­ди­на­ми­че­ски ус­той­чи­вы­ми. В лио­фоб­ных сис­те­мах взаи­мо­дей­ст­вие ме­ж­ду фа­за­ми сла­бое, для их об­ра­зо­ва­ния тре­бу­ют­ся энер­ге­тич. за­тра­ты. Лио­фоб­ные сис­те­мы тер­мо­ди­на­ми­че­ски не­ус­той­чи­вы, и их су­ще­ст­во­ва­ние воз­мож­но толь­ко бла­го­да­ря дей­ст­вию фак­то­ров ста­би­ли­за­ции.

Р. ши­ро­ко рас­про­стра­не­ны в при­ро­де и иг­ра­ют важ­ную роль в бы­ту, жиз­не­дея­тель­но­сти ор­га­низ­мов, во мно­гих от­рас­лях пром-cти и тех­ни­ки. Мож­но ска­зать, что все ок­ру­жаю­щие нас жид­ко­сти – Р., т. к. аб­со­лют­но чис­тых, не со­дер­жа­щих ни­ка­ких при­ме­сей жид­ко­стей не су­ще­ст­ву­ет. Р. слу­жат сре­дой, в ко­то­рой про­те­ка­ют мн. при­род­ные и пром. про­цес­сы. Час­то хи­мич. ре­ак­ции про­ис­хо­дят толь­ко в Р. Изу­че­ние фи­зи­ко-хи­мич. свойств Р. по­мо­га­ет со­вер­шен­ст­во­вать про­цес­сы раз­де­ле­ния и очи­ст­ки ве­ществ ме­то­да­ми рек­ти­фи­ка­ции, экс­трак­ции, кри­стал­ли­за­ции, ион­но­го об­ме­на, тер­мо­диф­фу­зии и др. Ис­поль­зо­ва­ние не­вод­ных Р. свя­за­но с при­ме­не­ни­ем по­ли­ме­ров, фор­мо­ва­ни­ем из них тон­ких плё­нок, мем­бран, по­лу­че­ни­ем кра­си­те­лей и ла­ков. Мн. ми­не­ра­лы, гор­ные по­ро­ды, а так­же про­дук­ты пи­та­ния (сли­воч­ное мас­ло, мо­ло­ко, мо­ро­же­ное), то­ва­ры бы­то­вой хи­мии и сред­ст­ва лич­ной ги­гие­ны (кре­мы, ма­зи, зуб­ные пас­ты) пред­став­ля­ют со­бой кол­ло­ид­ные рас­тво­ры.